Willingness to pay (Delta Methodology) + elasticities - Mixed logit models

[Louis Henri Furtado]

Dear Prof. Bierlaire, 

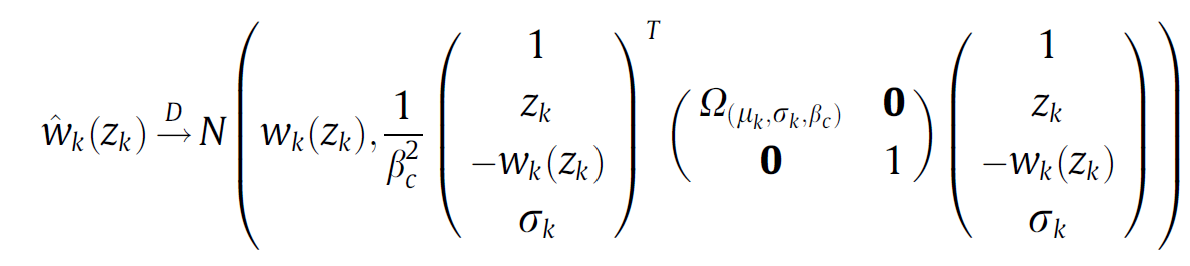
I am sorry to bother you again. 

After creating the utility functions for my mixed logit models, I am trying to calculate some indicators related to the cost parameter which is fixed. I have now two issues.

1. I followed your tutorial for the willingness to pay and I saw that we need to use the Derivate and then Estimate. Due to the fact that on the numerator I have a parameter that is normally distributed, how should I write the equation?

I was trying to use the Delta model (Reference: Chpater 5.2 of "Bliemer, M.C.J., & Rose, J.M. (2013). Confidence Intervals of Willingness-to-Pay for Random Coefficient Logit Models. Transportation Research Part B: Methodological, 58, 199-214. https://doi.org/10.1016/j.trb.2013.09.010.") and so incorporate it in the calculation in Biogeme:

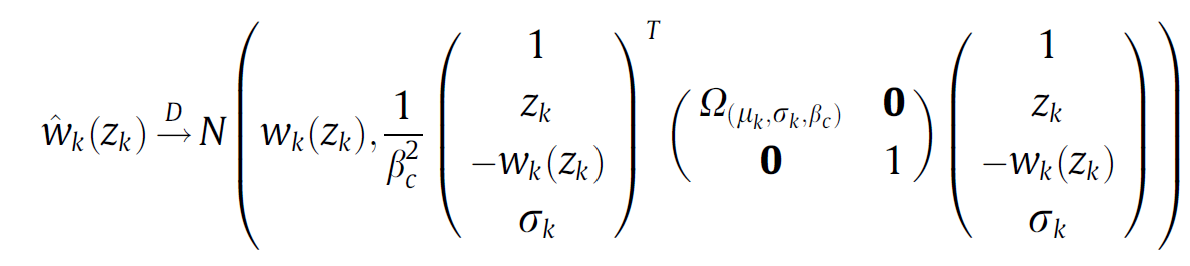
Would you give me any hint how to decompose this equation in order to write in Biogeme?

2. Regarding the elasticities for the cost parameter (fixed) but from mixed logit model, I have great differences in the results between the generic and logit elasticity. Whats does it means? Which one is the most representative that I should choose?

I thank you in advanced for your help!

Best Regards,

Louis Henri Furtado

[Bierlaire Michel]

On 10 Aug 2022, at 13:32, Louis Henri Furtado <tornado...@gmail.com> wrote:

Dear Prof. Bierlaire, 

I am sorry to bother you again. 

After creating the utility functions for my mixed logit models, I am trying to calculate some indicators related to the cost parameter which is fixed. I have now two issues.

1. I followed your tutorial for the willingness to pay and I saw that we need to use the Derivate and then Estimate. Due to the fact that on the numerator I have a parameter that is normally distributed, how should I write the equation?

I was trying to use the Delta model (Reference: Chpater 5.2 of "Bliemer, M.C.J., & Rose, J.M. (2013). Confidence Intervals of Willingness-to-Pay for Random Coefficient Logit Models. Transportation Research Part B: Methodological, 58, 199-214. https://doi.org/10.1016/j.trb.2013.09.010.") and so incorporate it in the calculation in Biogeme:

<Delta Method.png>

Would you give me any hint how to decompose this equation in order to write in Biogeme?

The best way is to use Monte-Carlo simulation. 

If your random vector w is N(wbar, Omega), you need to rewrite it as  wbar + L ksi, where L is the Cholesky factor of Omega, and ksi is a N(0, 1). Then, you draw from ksi.

 

2. Regarding the elasticities for the cost parameter (fixed) but from mixed logit model, I have great differences in the results between the generic and logit elasticity. Whats does it means? Which one is the most representative that I should choose?

Checking the validity of a model is a vast topic. Analyzing the elasticities is always a good idea, and they can be compared across models, and are not dependent on the scale (as the parameters). 

The fact that the mixed logit gives you suspicious results for the elasticity means that the specification should be revised. 

On a final note, if the number of draws is insufficient, the results are meaningless.

I thank you in advanced for your help!

Best Regards,

Louis Henri Furtado

--
You received this message because you are subscribed to the Google Groups "Biogeme" group.
To unsubscribe from this group and stop receiving emails from it, send an email to biogeme+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/biogeme/55dc2dac-7e7a-4422-a3c1-cefcf373a62an%40googlegroups.com.
<Delta Method.png>