Warning on big vowpal wabbit file

[Aleksey Astafiev]

Hello,

I've generated a vowpal wabbit format file about 300Mb file.

After that I use BatchVectorizer and getting such warnings:

[libprotobuf WARNING /Users/usual/PycharmProjects/artifint/bigartm/3rdparty/protobuf-3.0.0/src/google/protobuf/io/coded_stream.cc:604] Reading dangerously large protocol message. If the message turns out to be larger than 2147483647 bytes, parsing will be halted for security reasons. To increase the limit (or to disable these warnings), see CodedInputStream::SetTotalBytesLimit() in google/protobuf/io/coded_stream.h.

I'm concerned about how these warnings influence on final result in future. How could I safely tune parameters through BigARTM library? Does it mean the number of features generated in VW file  should be decreased?

[Oleksandr Frei]

Hi

Have you tried to reduce BatchVectorizer.batch_size parameter? Default is 1000, maybe try 100?

http://docs.bigartm.org/en/stable/api_references/python_interface/batches_utils.html#artm.BatchVectorizer.batch_size

The overall size of vowpal wabbit file is not a problem, BigARTM can handle very large VW files as input. But it your documents are too long that it will be a good idea to put less documents in each batch.

Out of curiosity, how many documents do you have in the vw file? Do you know how many unique words exist across your collection?

Alex

--
You received this message because you are subscribed to the Google Groups "bigartm-users" group.
To unsubscribe from this group and stop receiving emails from it, send an email to bigartm-users+unsubscribe@googlegroups.com.
To post to this group, send email to bigart...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/bigartm-users/c0969bfb-e249-4a70-92cd-28950f20f91d%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.

[Aleksey Astafiev]

Hi,

I'll try reduce batch_size parametr.

The answer on other questions is:

Find 3505338 unique tokens in 9587 items

[Aleksey Astafiev]

Update

batch_size=100 didn't solve warning issue

On Wednesday, July 19, 2017 at 12:05:17 PM UTC+3, Oleksandr Frei wrote:

Hi

Have you tried to reduce BatchVectorizer.batch_size parameter? Default is 1000, maybe try 100?

http://docs.bigartm.org/en/stable/api_references/python_interface/batches_utils.html#artm.BatchVectorizer.batch_size

The overall size of vowpal wabbit file is not a problem, BigARTM can handle very large VW files as input. But it your documents are too long that it will be a good idea to put less documents in each batch.

Out of curiosity, how many documents do you have in the vw file? Do you know how many unique words exist across your collection?

Alex

On Wed, Jul 19, 2017 at 10:54 AM, Aleksey Astafiev <aast...@gmail.com> wrote:

Hello,

I've generated a vowpal wabbit format file about 300Mb file.

After that I use BatchVectorizer and getting such warnings:

[libprotobuf WARNING /Users/usual/PycharmProjects/artifint/bigartm/3rdparty/protobuf-3.0.0/src/google/protobuf/io/coded_stream.cc:604] Reading dangerously large protocol message. If the message turns out to be larger than 2147483647 bytes, parsing will be halted for security reasons. To increase the limit (or to disable these warnings), see CodedInputStream::SetTotalBytesLimit() in google/protobuf/io/coded_stream.h.

I'm concerned about how these warnings influence on final result in future. How could I safely tune parameters through BigARTM library? Does it mean the number of features generated in VW file  should be decreased?

--
You received this message because you are subscribed to the Google Groups "bigartm-users" group.

To unsubscribe from this group and stop receiving emails from it, send an email to bigartm-user...@googlegroups.com.

[Oleksandr Frei]

I see. I think you should just ignore this warning. It is really confusing because the warnings appears whenever there is a batch exceeds 32 MB, while the library will work just fine with batches up to 2 GB in size. 

https://github.com/bigartm/bigartm/blob/def8d3942bd275910bf3243e969575a5963784e6/3rdparty/protobuf-3.0.0/src/google/protobuf/io/coded_stream.h#L627

>3505338 unique tokens in 9587 items

Are these tokens n-grams or similar? Generally I would say this is a very large dictionary for a small collection. Have you tried to filter out tokens that appear in one document (or too few documents, let's say 2 or 5)? Without changing your Vowpal Wabbit input file you may ask BigARTM to filter the dictionary, and use the filtered dictionary to create artm.ARTM model:

A tutorial which describe filtering:

https://github.com/bigartm/bigartm-book/blob/master/ARTM_tutorial_RU.ipynb

And generally these are the steps:

batch_vectorizer = artm.BatchVectorizer(data_path='',

                                        data_format='bow_uci',

                                        collection_name='my_collection',

                                        target_folder='my_collection_batches')

my_dictionary = artm.Dictionary()

my_dictionary.gather(data_path='my_collection_batches')

my_dictionary.filter(min_tf=10, max_tf=2000, min_df_rate=0.01)  # see http://docs.bigartm.org/en/stable/api_references/python_interface/dictionary.html#artm.Dictionary.filter for description of the parameters

model = artm.ARTM(num_topics=20, dictionary=my_dictionary)

# now you have reduced set of tokens in artm.ARTM model, based on custom min_tf, max_tf, min_df_rate thresholds)

Kind regards,

Alex

To unsubscribe from this group and stop receiving emails from it, send an email to bigartm-users+unsubscribe@googlegroups.com.

To post to this group, send email to bigart...@googlegroups.com.

To view this discussion on the web visit https://groups.google.com/d/msgid/bigartm-users/358235eb-bae3-4537-b75a-d6e6616ac3ae%40googlegroups.com.

[Aleksey Astafiev]

Yes. This tokens are ngrams. From 2 to 6. That is why I'm getting such a big dictionary. 

Yes. I've tried to filter tokens using min_tf=2, max_df_rate=0.01 (this I think the most applicable in my case) but still getting same warnings. This reduce me the dictionary but not enough  

Moreover, when using bigartm filtering i'm getting this warning in bigartm logs:

Error in perplexity dictionary for token перевозка_утвердить, class @text (and potentially for other tokens). Verify that the token exists in the dictionary and it's value > 0. Document unigram model will be used for this token (and for all other tokens under the same conditions).

I understand this happens because of filtering and if I tune my vw file i wouldn't get such warning. But this is confusing too. Could you tell what exactly will do library in this case, that describes in this phrase "Document unigram model will be used for this token..." ?

[Oleksandr Frei]

> I've tried to filter tokens using min_tf=2, max_df_rate=0.01 (this I think the most applicable in my case) but still getting same warnings

The warning is still expected because filtering does not reduce the size of the batches. Only the number of the tokens in the model is reduced.

>Document unigram model will be used for this token

This applies to the way BigARTM calculates perplexity, and is briefly explained here http://docs.bigartm.org/en/stable/tutorials/scores_descr.html. The formula is as follows:

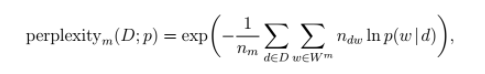
http://www.MachineLearning.ru/wiki/images/d/d5/Voron17survey-artm.pdf (page 36, chapter 12)

Now think what happens if p(w|d)==0 --- can't calculate logarithm. This case actually happens, especially for sparse models, because p(w|d) is calculated as \sum_t p(w|t)*p(t|d) -- and it could be that for all topics either $p(w|t)==0$ or $p(t|d) == 0$.  There are 3 ways to handle p(w|d)==0.

1. Completely exclude p(w|d)==0 summands from the perplexity formula 

2. Approximate p(w|d) = n_dw / n_d   (how many times $w$ has occurred in a given document $d$ divided by the length of $d$ in words) --- this BigARTM calls "document unigram model".

3. Approximate p(w|d) = tf(w)   (how many times $w$ occurred in the entire collection divided by the length of the collection in words) - this BigARTM calls "collection unigram model".

Method (1) may give low perplexity, e.g. too optimistic - for example extremely sparse models will tend to have perplexity close to 0 despite being very bad

Method (2) is better than (1), but still gives too optimistic perplexity 

Method (3) gives a conservative estimate of perplexity, but it requires to know tf -- e.g. frequency in the dictionary.

The warning that you get indicates that BigARTM tried to use method (3), and fall back to method (2) because the token was not present in the dictionary so its tf is unknown. For you it means that your perplexity score might be slightly underestimated.

Kind regards,

Alex

To unsubscribe from this group and stop receiving emails from it, send an email to bigartm-users+unsubscribe@googlegroups.com.

To post to this group, send email to bigart...@googlegroups.com.

To view this discussion on the web visit https://groups.google.com/d/msgid/bigartm-users/f4768a96-e3d8-4eec-8847-b1b9884fd359%40googlegroups.com.

[Aleksey Astafiev]

Thank you much!

Know it's clear. Will try further.