Simple, more robust method to assess agreement

[Abhaya Indrayan]

The Bland-Altman method has been extremely successful in making us aware of the difference between an agreement in individual values and agreement in aggregates. It requires calculating an interval (mean of differences +- 2SD of differences) and interpret it against the prespecified clinical tolerance limits based on, if I may say so, medical "equivalence". These pre-specified clinical tolerance limits can be directly used to find the extent of agreement. This procedure is non-parametric (does not require differences to follow Gaussian distribution), flexible, and simple. The preprint with complete details is available at  https://www.preprints.org/manuscript/202108.0343/v1 

I have tried a couple of journals but they have rejected without giving reasons. There must be something desperately wrong with this direct method but I would appreciate if I am told what is wrong?

Thanks.

~Abhaya

--

Dr Abhaya Indrayan

Personal website: http://indrayan.weebly.com

[Sreenivas.V]

Dear Prof. Indrayan,

What you conveyed in the manuscript provides a direct quantification of the agreement as per the predefined limits.

Medical journal editors have strange ways of seeing things.  I remember in one case we gave the frequency distribution of the differences, the editor was happy to see such presentation.   But a recent such presentation was forced to be removed and we were asked strictly to follow B-A plot analysis only (Strategies in Trauma Limb Reconstruction Journal).  The reviewers were adamant and refused to buy the argument that we are providing additional information (proportion of cases within predefined clinically acceptable limits along with 95% CI).  Finally the lead author, a budding young faculty removed this description.

I also feel it will be a useful method, may be better than B-A method as it quantifies the agreement.  One important thing is B-A plot shows any biases in the comparisons, but doesn’t help in quantifying.

You may keep trying with other journals show casing it as an another way of looking agreement in addition to the standard B-A plots.

Best wishes & regards

Sreenivas

--
--
To post a new thread to MedStats, send email to MedS...@googlegroups.com .
MedStats' home page is http://groups.google.com/group/MedStats .
Rules: http://groups.google.com/group/MedStats/web/medstats-rules

---
You received this message because you are subscribed to the Google Groups "MedStats" group.
To unsubscribe from this group and stop receiving emails from it, send an email to medstats+u...@googlegroups.com.
To view this discussion on the web, visit https://groups.google.com/d/msgid/medstats/CAP7G4a7uF-0%3D3soSkqpA4fLJHRST3LrcxD91xwa5L9uD8zHHEw%40mail.gmail.com.

--

Professor
Department of Biostatistics
All India Institute of Medical Sciences
New Delhi 110029

https://scholar.google.co.in/citations?hl=en&user=6unT1oYAAAAJ

https://www.ncbi.nlm.nih.gov/pubmed/?term=”V. Sreenivas” or “Sreenivas. V” OR “V Sreenivas” OR “Sreenivas V” OR “S Vishnubhatla” or “S. Vishnubhatla” OR “Vishnubhatla. S” OR “Vishnubhatla S” OR "Vishnubhatla Sreenivas" OR "Sreenivas Vishnubhatla" 

[Bunce, Catey]

I think the problem is with the journals rather than the method.

 

Best wishes

 

Catey

--

[Abhaya Indrayan]

Yes, Catey, it seems the journals do not want to entertain a more robust, easy, and flexible method than the prevalent and widely accepted Bland-Altman method for assessing quantitative agreement. Now that the method is available over the internet, I hope at least some will take a note.

Regards.

~Abhaya

--

Dr Abhaya Indrayan

Personal website: http://indrayan.weebly.com

To view this discussion on the web, visit https://groups.google.com/d/msgid/medstats/VE1PR01MB5792130A391702A032706428AEC39%40VE1PR01MB5792.eurprd01.prod.exchangelabs.com.

[Thomas Keller]

Dear Prof Indrayan,

your paper is quite interesting.

- I can give you some feedbacjk from clin chem and lab medicine perspective, and having the CLSI guideline EP09A3 in mind.

- I think we should distinguish between bias (which refers to the mean of differences) and imprecision, the latter is more complex, since precision of both methods influences the range.

- As long as possible we should work with parametric approaches. I have done a lot of method comparisons in laboratory medicine, and due to my experience, if the difference plot works (so when we have homogeneity of StdDevs or CVs) we can use the parametric way. Otherwise we have to switch to regression methods (Deming regression, Passing Bablok regression and estimate the bias for specific, important concentrations.

- In regard of equivalence testing the main problem is the definition of the acceptance criteria. In the clin chem community, three concepts are discussed: state of the art, biological variablilty or diagnostic consequence, see Ceriotti et al, CCLM 2016, Criteria for assigning .... analytical performnce specifications.... Practically it is really difficult to introduce the equivalence test approach, sind the known acceptance criteria (e. g. "10% for ELISA assays") lead to very large sample sizes - so widely  used criteria have to be discussed. 

- Tolerance intervals intervals are mentiond in the paper of Barnhart et al, 2007, J Biopharm Stat. 17, 529

- In parts of current literature (e. g. the book from Chouhary: measuring agreemen) however the BA-plot is criticized in general and application of mixed models is requested.

Kind regards

Thomas
www.acomed-statistik.de

[Abhaya Indrayan]

Thanks to Dr Thomas Keller for providing useful inputs from the lab medicine perspective. 

Bias and precision can be obtained under my method also although they are not required for assessing the extent of agreement. This is mentioned in the paper.

The parametric approach is fine so long as the conditions are fulfilled. Otherwise it can mislead. 

Bernhart et al. have mentioned tolerance interval based on confidence level whereas I am advocating clinical tolerance interval. Please note that a clinical tolerance interval is required to interpret agreement under BA method also.

Warm regards.

~Abhaya

--

Dr Abhaya Indrayan

Personal website: http://indrayan.weebly.com

[Bruce Weaver]

For cases like the blood glucose example in Dr. Indrayan's preprint, I like to give readers the following:

• A scatter-plot that includes both the line of equality (Y=X) and the least squares regression line
• The ICC, Pearson r, and the mean difference, each with its 95% CI

It would not be difficult to add two more lines indicating the clinical tolerance limits, and the proportion of data points falling within those limits.  I've pasted below some Stata code to do that for Dr. Indrayan's example.  Here are the main results.  The reddish line in the graph below is the OLS regression line, and the dashed lines show the tolerance limits (-2 and 5).  (I didn't take the time to format everything like one would for an article, but I hope it is still understandable.) 

ICC = .988 (.977 to .993)

Pearson r = 0.990 (0.981 to 0.995)

Mean diff = 1.975 (.570 to 3.380)

Proportion within limits using all observations = .900 (.769 to .973) [Wilson CI]

Proportion within limits excluding the outlier = .923 (.797 to .973) [Wilson CI]

In this example, the ICC and Pearson r values are very similar, and the mean difference, although significant at the .05 level (if one can still say such things!) is fairly small.  That suggests to me that there is pretty good absolute agreement.  When ICC < Pearson r, a plot like this allows one to determine the reason for that:  I.e., is it due to a mean difference, a weak linear relationship, or both?  All of that is easily visible in such a plot, I think.  Adding dashed lines for the clinical tolerance limits (and the accompanying proportion with CI) is just more useful information for the reader, IMO.  YMMV.

Cheers,

Bruce

Stata Code

// Data from Table 1 in Abhaya Indrayan's 2021 preprint:
// https://www.preprints.org/manuscript/202108.0343/v1

clear *
input byte id meth1 meth2 diff pcdiff
1 106 110 4 3.77
2 82 80 -2 -2.44
3 121 126 5 4.13
4 95 97 2 2.11
5 178 199 21 11.80
6 147 145 -2 -1.36
7 135 138 3 2.22
8 140 139 -1 -0.71
9 112 115 3 2.68
10 126 130 4 3.17
11 130 129 -1 -0.77
12 106 105 -1 -0.94
13 187 195 8 4.28
14 77 80 3 3.90
15 120 124 4 3.33
16 118 121 3 2.54
17 67 65 -2 -2.99
18 136 141 5 3.68
19 98 99 1 1.02
20 102 105 3 2.94
21 118 121 3 2.54
22 182 180 -2 -1.10
23 167 160 -7 -4.19
24 132 135 3 2.27
25 82 82 0 0.00
26 79 80 1 1.27
27 139 138 -1 -0.72
28 125 127 2 1.60
29 119 118 -1 -0.84
30 78 83 5 6.41
31 131 132 1 0.76
32 145 143 -2 -1.38
33 169 172 3 1.78
34 158 157 -1 -0.63
35 144 145 1 0.69
36 138 137 -1 -0.72
37 121 131 10 8.26
38 107 106 -1 -0.93
39 125 127 2 1.60
40 138 142 4 2.90
end

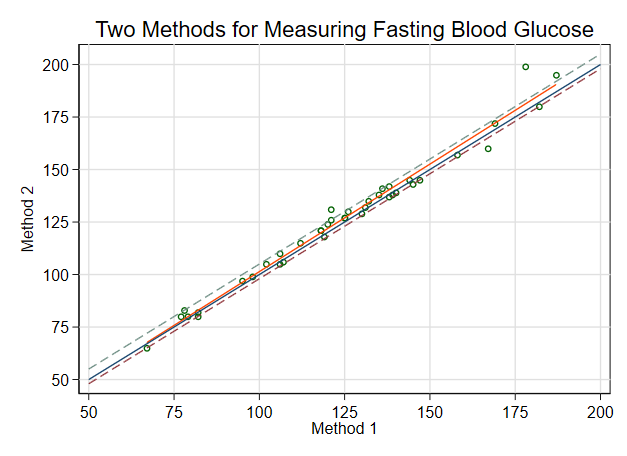
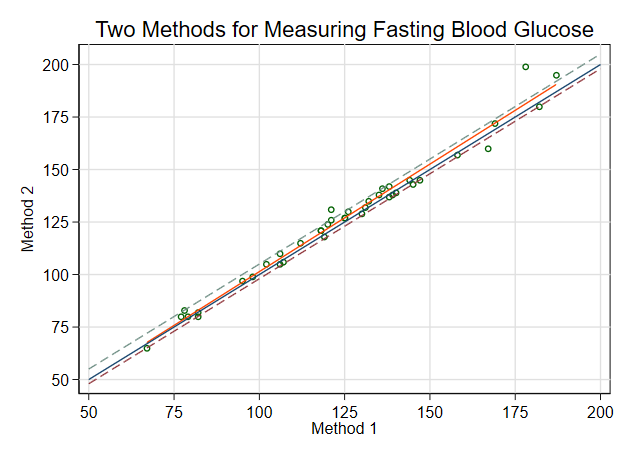
twoway scatter meth2 meth1, ///
xlab(50(25)200, grid) ylab(50(25)200, grid angle(0)) ///
ms(oh) xtitle(Method 1) ytitle(Method 2) || ///
lfit meth2 meth1 || ///
function y=x, range(50 200) || ///
function y=x-2, range(50 200) lpattern(dash) || ///
function y=x+5, range(50 200) lpattern(dash) legend(off) ///
title(Two Methods for Measuring Fasting Blood Glucose)

generate byte good = inrange(meth2,meth1-2,meth1+5)
* ssc install fre // Uncomment this line to install -fre- command if necessary
fre good
ci proportion good, wilson
ci proportion good if inrange(meth1-meth2,-10,10), wilson
ttest meth2==meth1
corrci meth*

// Reshape to long before using -icc- command
reshape long meth, i(id) j(m)
icc meth id

[Abhaya Indrayan]

Thanks to Bruce for his valuable inputs. These will surely help. I will try to incorporate his suggestions with due acknowledgment.

~Abhaya

--

Dr Abhaya Indrayan

Personal website: http://indrayan.weebly.com

--
--
To post a new thread to MedStats, send email to MedS...@googlegroups.com .
MedStats' home page is http://groups.google.com/group/MedStats .
Rules: http://groups.google.com/group/MedStats/web/medstats-rules

---
You received this message because you are subscribed to the Google Groups "MedStats" group.
To unsubscribe from this group and stop receiving emails from it, send an email to medstats+u...@googlegroups.com.

To view this discussion on the web, visit https://groups.google.com/d/msgid/medstats/7a4c8dec-7e61-4698-bf53-63a47fadb39an%40googlegroups.com.

[Bruce Weaver]

In my earlier post, I failed to mention that -corrci- is a user-written command for Stata (by Nick Cox).  Here is the command to install it:

net install pr0041_3.pkg // Install NJC's -corrci- command 

[Abhaya Indrayan]

OK. Thanks.

To view this discussion on the web, visit https://groups.google.com/d/msgid/medstats/b8704971-5e73-485e-9e19-ee73546c9442n%40googlegroups.com.

[Bunce, Catey]

Sometimes less is more. 

 

Best wishes to all

 

Catey

 

From: meds...@googlegroups.com <meds...@googlegroups.com> On Behalf Of Abhaya Indrayan
Sent: 24 August 2021 16:49
To: meds...@googlegroups.com
Subject: Re: {MEDSTATS} Simple, more robust method to assess agreement

 

OK. Thanks.

 

On Tue, Aug 24, 2021 at 9:17 PM Bruce Weaver <bwe...@lakeheadu.ca> wrote:

In my earlier post, I failed to mention that -corrci- is a user-written command for Stata (by Nick Cox).  Here is the command to install it:

 

net install pr0041_3.pkg // Install NJC's -corrci- command 

 

 

 

On Tuesday, August 24, 2021 at 11:37:05 AM UTC-4 aindrayan wrote:

Thanks to Bruce for his valuable inputs. These will surely help. I will try to incorporate his suggestions with due acknowledgment.

 

~Abhaya

--

Dr Abhaya Indrayan

Personal website: http://indrayan.weebly.com

 

On Tue, Aug 24, 2021 at 8:58 PM Bruce Weaver <bwe...@lakeheadu.ca> wrote:

For cases like the blood glucose example in Dr. Indrayan's preprint, I like to give readers the following:

• A scatter-plot that includes both the line of equality (Y=X) and the least squares regression line
• The ICC, Pearson r, and the mean difference, each with its 95% CI

It would not be difficult to add two more lines indicating the clinical tolerance limits, and the proportion of data points falling within those limits.  I've pasted below some Stata code to do that for Dr. Indrayan's example.  Here are the main results.  The reddish line in the graph below is the OLS regression line, and the dashed lines show the tolerance limits (-2 and 5).  (I didn't take the time to format everything like one would for an article, but I hope it is still understandable.) 

 

To view this discussion on the web, visit https://groups.google.com/d/msgid/medstats/CAP7G4a4UUMCmJrd1j0LSq6Wusqt5ryQQEDVv4Vx1J8K_fQhbDw%40mail.gmail.com.