Re: Rhat and rank normalization
49 views
Skip to first unread message
Andrew Gelman
Aug 20, 2014, 12:14:48 PM8/20/14
to Aki Vehtari, stan...@googlegroups.com
[ccing stan-dev]
Hi, Aki. Yes, I went through similar thoughts. The rank normalization is more robust but throws away information, which led be to be a bit uncertain about what to do and what to recommend.
A
On Aug 18, 2014, at 9:05 PM, Aki Vehtari <Aki.V...@aalto.fi> wrote:
> Hi,
>
> I've been reading old Stan list messages posted during my vacation, and wanted to say that I think the rank normalisation (rank + z-score) is sensible thing to do. It is routinely used in epidemiological literature to transform very skewed distributions (which are common in biological measurements) before fitting imputation models. On the other hand, I'm bit worried that rank normalisation may throw away information. Distribution of lp may have very long tail, and you've seen that Rhat for lp is often higher. Rank normalisation would transform the samples far from the tail to be more "normal" throwing away the information about that some values are extreme.
>
> Aki
Hi, Aki. Yes, I went through similar thoughts. The rank normalization is more robust but throws away information, which led be to be a bit uncertain about what to do and what to recommend.
A
On Aug 18, 2014, at 9:05 PM, Aki Vehtari <Aki.V...@aalto.fi> wrote:
> Hi,
>
> I've been reading old Stan list messages posted during my vacation, and wanted to say that I think the rank normalisation (rank + z-score) is sensible thing to do. It is routinely used in epidemiological literature to transform very skewed distributions (which are common in biological measurements) before fitting imputation models. On the other hand, I'm bit worried that rank normalisation may throw away information. Distribution of lp may have very long tail, and you've seen that Rhat for lp is often higher. Rank normalisation would transform the samples far from the tail to be more "normal" throwing away the information about that some values are extreme.
>
> Aki
Michael Betancourt
Aug 20, 2014, 5:11:09 PM8/20/14
to stan...@googlegroups.com
Isn’t any estimator that just uses first and second moments throwing away information?
The rank normalization is just getting the p-values right (correctly calibrating the PSRF to be
more in line with Andrew’s perspective) and not hemorrhaging more information, no?
> --
> You received this message because you are subscribed to the Google Groups "stan development mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-dev+u...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
The rank normalization is just getting the p-values right (correctly calibrating the PSRF to be
more in line with Andrew’s perspective) and not hemorrhaging more information, no?
> You received this message because you are subscribed to the Google Groups "stan development mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-dev+u...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
Andrew Gelman
Aug 21, 2014, 4:25:54 AM8/21/14
to stan...@googlegroups.com
M
It depends on the scenario. As with all robust methods, what we’re doing will work better in some settings (e.g., the posterior for a Cauchy-distributed quantity of interest) but not so well in others. There’s also the issue that we currently report the posterior mean and its s.e., and these are best estimated by the moments on the original scale. Another option would be for us to bury the posterior mean and instead lead with the posterior median and an estimate of its uncertainty.
A
It depends on the scenario. As with all robust methods, what we’re doing will work better in some settings (e.g., the posterior for a Cauchy-distributed quantity of interest) but not so well in others. There’s also the issue that we currently report the posterior mean and its s.e., and these are best estimated by the moments on the original scale. Another option would be for us to bury the posterior mean and instead lead with the posterior median and an estimate of its uncertainty.
A
Michael Betancourt
Aug 21, 2014, 4:30:17 AM8/21/14
to stan...@googlegroups.com
In the asymptotic regime where the Monte Carlo CLT kicks in the median and mean are equivalent. What to do in the transient regime is somewhat ill-posed, although some could interpret that freedom as a feature.
Aki Vehtari
Aug 21, 2014, 6:39:59 AM8/21/14
to Andrew Gelman, stan...@googlegroups.com
Have you thought about making some simulation studies?
1) sample from Gaussian using MCMC (so it is easy to control autocorrelation
and convergence etc.)
2) transform samples to Chi^2_k distribution with varying k (simulating
samples from lp)
3) rank normalise samples from (2)
Compare Rhat computed from 1, 2, and 3
This should give some idea how to proceed?
Aki
1) sample from Gaussian using MCMC (so it is easy to control autocorrelation
and convergence etc.)
2) transform samples to Chi^2_k distribution with varying k (simulating
samples from lp)
3) rank normalise samples from (2)
Compare Rhat computed from 1, 2, and 3
This should give some idea how to proceed?
Aki
Andrew Gelman
Aug 21, 2014, 10:03:35 AM8/21/14
to stan...@googlegroups.com
No, the mean and median are not equivalent for example for a quantity of interest with a Cauchy posterior.
Ben Goodrich
Aug 21, 2014, 1:48:18 PM8/21/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
On Thursday, August 21, 2014 4:25:54 AM UTC-4, Andrew Gelman wrote:
It depends on the scenario. As with all robust methods, what we’re doing will work better in some settings (e.g., the posterior for a Cauchy-distributed quantity of interest) but not so well in others. There’s also the issue that we currently report the posterior mean and its s.e., and these are best estimated by the moments on the original scale. Another option would be for us to bury the posterior mean and instead lead with the posterior median and an estimate of its uncertainty.
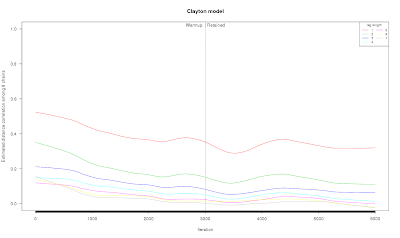
If you want to know a PSRF for a particular margin of interest, then I think you have to use the original scale. If you are using the Rhats to decide if the chains have converged to the posterior distribution, then maybe transformations help in some cases but it is not so hard to fool it. One way is to draw from a posterior that has standard normal margins and a sufficiently evil copula density, such as the bivariate Clayton
parameters {
real z[2];
real<lower=0> delta;
}
model {
real theta;
real p[2];
theta <- delta - 1;
z ~ normal(0,1);
delta ~ normal(0,1);
p[1] <- Phi(z[1]);
p[2] <- Phi(z[2]);
increment_log_prob( log1p(theta) -
(1 + theta) * log(p[1] * p[2]) -
(1 + 2 * theta) / theta * log(pow(p[1], -theta) + pow(p[2], -theta) - 1) );
}
With 8 chains, 6000 iterations, and a seed of 12345, you get small Rhats on the original scale
> Clayton
Inference for Stan model: Clayton.
8 chains, each with iter=6000; warmup=3000; thin=1;
post-warmup draws per chain=3000, total post-warmup draws=24000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
z[1] 0.06 0.03 1.00 -1.93 -0.62 0.05 0.73 1.98 1490 1.01
z[2] -0.01 0.03 1.02 -2.01 -0.71 -0.02 0.71 2.02 1359 1.00
delta 0.88 0.02 0.58 0.10 0.43 0.76 1.22 2.28 1003 1.01
lp__ -1.74 0.02 1.16 -4.83 -2.23 -1.43 -0.91 -0.37 2941 1.00
and on the rank-normalized scale
> rank_rhats(Clayton)
Inference for the input samples (8 chains: each with iter=3000; warmup=0):
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
z[1] 0 0.03 1 -1.96 -0.67 0 0.67 1.96 1537 1.01
z[2] 0 0.03 1 -1.96 -0.67 0 0.67 1.96 1371 1.00
delta 0 0.05 1 -1.96 -0.67 0 0.67 1.96 482 1.02
lp__ 0 0.03 1 -1.96 -0.67 0 0.67 1.96 1193 1.00
but the chains do not converge, in part because they get stuck
which Mike's preferred method would catch because n_divergent__ is usually not zero and my preferred method would catch because with a thin interval of 6
> convergence_test(Clayton, thin = 6, R = 199)
[1] "Multivariate loss = 1.005"
disco(x = posterior, factors = data.frame(chain_id), R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
chain_id 15 49.03718 3.26915 2.734 0.005
Within 3984 4764.27077 1.19585
Total 3999 4813.30795
So, I am still searching for a case
https://groups.google.com/d/msg/stan-dev/lMy2CZJD9fk/JtjzFw3AUx0J
as to why using Rhats to decide the question of whether the chains have converged to the stationary distribution is better than what I am favoring.
Ben
Reply all
Reply to author
Forward
0 new messages