interp1-like functionality from Grid.jl

[Spencer Lyon]

I need to do some basic interpolation and think Grid.jl should provide all the functionality I need, but I can’t quite get it to work for me.

I am essentially looking to do something like what is described for this form of the interp1 matlab function (copied and pasted excerpt from documentation):

Vq = interp1(X,V,Xq) interpolates to find Vq, the values of the underlying function V=F(X) at the query points Xq. X must be a vector of length N.

A minimal example from the Matlab docs (slightly adapted) of what I would like to do is

X = 3:15; 
V = sin(X); 
Xq = 4:.25:12;
Vq = interp1(X,V,Xq);

Here is what I have so far in Julia:

X = [3:15]
V = sin(X);
Xq = [4:.25:12]

ig = InterpGrid(V, BCnil, InterpLinear)

As far as I understand, I can now “index” the ig object to do interpolation. The problem I am having is that the portion of the grid I would like to interpolate over, Xq, is not represented in terms of indexes, but rather points on the interval [minimum(X), maximum(X)].

What do I need to do to evaluate the function underlying ig at the grid points Xq?

[Stefan Schwarz]

you can go just like:

    y=[ig[x] for x in Xq]; # evaluate using list comprehension

and using PyPlot's plot:

    plot(Xq, y)

     

if you want to smooth the plot you can use e.g.  InterpQuadratic and increase you Xg:

    X = [3:15]

    V = sin(X);

    Xq = [4:.05:12]

    ig = InterpGrid(V, BCnil, InterpQuadratic);

    plot(Xq, [ig[x] for x in Xq])

hope that helps.

     

[Tim Holy]

If I understand correctly, what you're missing is the ability to have a array
of values that is regularly-spaced but does not start at x=1. You have several
options:
- Just subtract 2 from all your Xq values.
- Create a type
immutable ShiftedInterpGrid{T,N,BC,IT}
IG::InterpGrid{T,N,BC,IT}
offset::Vector{T}
end
and define getindex() for this type to do the subtraction for you and pass
the "real" work onto IG. You could also scale the values if they aren't
usually spaced by 1.
- Use the (undocumented and incomplete) InterpIrregular (see interp.jl),
ig = InterpIrregular([X,], V, BCnil, InterpLinear)

The latter will be slower than either of the other two, simply because there
is more computation required for irregular grids than for regular ones.

--Tim

[Spencer Lyon]

Hey Stefan, thanks for the reply. That was the type of functionality I was hoping for, but it doesn’t quite work like we are expecting.

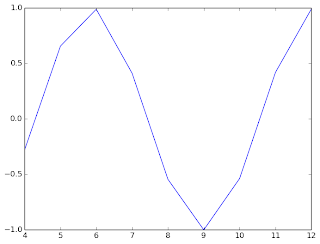
While the “interpolated” data does look like a sin wave, it is not even close to in the right place.

See what happens if we plot the actual grid points used to çreate the ig object (X, and V) with the interpolated values as well as the actual values of sin(Xq).

X = [3:15];
V = sin(X);
Xq = [4:.25:12];
ig = InterpGrid(V, BCnil, InterpLinear);

y=[ig[x] for x in Xq];

plot(X,V,"o",Xq,y, "orange", Xq, sin(Xq), "red");

legend(["Data", "Interp", "Actual"])

[Spencer Lyon]

Hey Tim,

Looks like that worked well:

X = [3:15];
V = sin(X);
Xq = [4:.25:12];
ig = InterpGrid(V, BCnil, InterpLinear);
y=[ig[x - 2.0] for x in Xq];
plot(X,V,"o",Xq,y, "orange", Xq, sin(Xq), "red");
legend(["Data", "Interp", "Actual"])

[Spencer Lyon]

Also,

The getindex method for the InterpGrid object can accept more than one point. There is no need to evaluate the points using a comprehension:

julia> y2 = ig[Xq - 2.0];

julia> y=[ig[x - 2.0] for x in Xq];

julia> maximum(y - y2)
0.0

julia> minimum(y - y2)
0.0

[Spencer Lyon]

Also Tim,

I am not sure I understand what you mean by

You could also scale the values if they aren’t usually spaced by 1.

This example now fails again:

X = [3:0.5:15];
V = sin(X);
Xq = [4:.25:12];
ig = InterpGrid(V, BCnil, InterpLinear);
y = ig[Xq - 2.0]
plot(X,V,"o",Xq,y, "orange", Xq, sin(Xq), "red");
legend(["Data", "Interp", "Actual"])

[Tim Holy]

On Tuesday, April 15, 2014 04:38:01 AM Spencer Lyon wrote:
> I am not sure I understand what you mean by
>
> You could also scale the values if they aren’t usually spaced by 1.

Basically, any time your values are evenly spaced, there is a linear mapping
x->xi from "physical" coordinates x to "indexing" coordinates xi, where x[1]
corresponds to xi=1 and x[n] corresponds to xi=n. It's just a question of
solving the equations

1 = m*x[1] + b
n = m*x[n] + b

for m and b. Then you can use ig[m*x+b] to evaluate at "physical" locations.

--Tim

[Spencer Lyon]

Thanks for the response. I think I have settled on how to get this to work. This is what I have right now

immutable ShiftedInterpGrid{T,N,BC,IT}
    IG::InterpGrid{T,N,BC,IT}
    m::Number
    b::Number
end

function ShiftedInterpGrid{T,BC,IT}(V::Vector{T}, X::Vector{T}, ::Type{BC}, ::Type{IT})
    n = size(X, 1)
    (b, m) = [1 X[1]; 1 X[n]] \ [1; n]
    IG = InterpGrid(V, BC, IT)
    ShiftedInterpGrid(IG, m, b)
end

function getindex{T,R<:Real}(G::ShiftedInterpGrid{T,1}, x::AbstractVector{R})
    s_x::AbstractVector{R} = G.b .+ G.m.*x
    return getindex(G.IG, s_x)
end

function getindex{T,R<:Real}(G::ShiftedInterpGrid{T,1}, x::R)
    s_x::R = G.b + G.m * x
    return getindex(G.IG, s_x)
end

It seems to me that this would be fairly standard functionality. I am sure there is a benefit to having the default getindex methods deal in “index units” instead of physical ones, but I can’t tell what that benefit is? Is there a reason you chose to have it set up the way it is?

Thanks again,

Spencer

[Tim Holy]

On Tuesday, April 15, 2014 05:35:27 AM Spencer Lyon wrote:
> It seems to me that this would be fairly standard functionality. I am sure
> there is a benefit to having the default getindex methods deal in “index
> units” instead of physical ones, but I can’t tell what that benefit is? Is
> there a reason you chose to have it set up the way it is?

When physical units = indexing units, you save one multiply and one add on
each interpolation operation. So it's best to implement the base operation
"minimally," and add wrapper types that require more operations around it.
I've not personally ever needed anything else (I mostly do interpolation on
images), and no one else has added it to Grid, either.

If you wanted to add your wrapper type to Grid, I think that would be great.
Some additional things to think about:
- Derivatives (here, the chain rule is your friend)
- Dimensions higher than 1
- It's no longer just a shift, it's also scaled, so a name change might be in
order.

--Tim

[Spencer Lyon]

I'd love to beef up this wrapper type and add it to grid, but unfortunately I wont' be able to get to it for a while -- probably late June. 

[Tim Holy]

That's fine. That's how it always works; things happen in Julia when someone
finds the time to do them.

--Tim

[Simon Byrne]

I actually wanted this functionality myself. See

https://github.com/timholy/Grid.jl/pull/14

[argel....@ciencias.unam.mx]

Cant get it to work, maybe i'm not understanding something. Can you help me?
On Julia V 4.0.2:

AltInterp = CoordInterpGrid(Znw,squeeze(Altura_segun_corte[xx,yy,:],(1,2)),BCnil,InterpLinear);

throws:

ERROR: LoadError: MethodError: `convert` has no method matching convert(::Type{Grid.CoordInterpGrid{T<:AbstractFloat,N,BC<:Grid.BoundaryCondition,IT<:Grid.InterpType,R}}, ::Array{Float64,1}, ::Array{Float64,1}, ::Type{Grid.BCnil}, ::Type{Grid.InterpLinear})
This may have arisen from a call to the constructor Grid.CoordInterpGrid{T<:AbstractFloat,N,BC<:Grid.BoundaryCondition,IT<:Grid.InterpType,R}(...),
since type constructors fall back to convert methods.
Closest candidates are:
  Grid.CoordInterpGrid{N,T<:AbstractFloat}(::NTuple{N,Range{T}}, ::Array{T<:AbstractFloat,N}, ::Any...)
  Grid.CoordInterpGrid{R<:Range{T},T<:AbstractFloat}(::R<:Range{T}, ::Array{T<:AbstractFloat,1}, ::Any...)
  call{T}(::Type{T}, ::Any)
  ...
 in call at essentials.jl:57
 [inlined code] from Cortes_horizontales_U_V_mod2.jl:46
 in anonymous at no file:0
 in include at ./boot.jl:261
 in include_from_node1 at ./loading.jl:304
while loading Cortes_horizontales_U_V_mod2.jl, in expression starting on line 42

I can't understand nothing from this error message! my variables in here are:
 

 julia> typeof(Znw)
Array{Float64,1}

julia> typeof(squeeze(Altura_segun_corte[1,1,:],(1,2)))
Array{Float64,1}

julia> sizeof(Znw)
224

julia> sizeof(squeeze(Altura_segun_corte[1,1,:],(1,2)))
224

What would the problem be?

[Tim Holy]

Now you should probably be using Interpolations.jl.

--Tim

On Wednesday, January 20, 2016 05:35:53 PM argel....@ciencias.unam.mx
wrote:

[Argel Ramírez Reyes]

Thanks, Tim!

--

Argel Ramírez R.
Licenciatura en física.

Facultad de ciencias - UNAM.