isomorphism in the real world
141 views
Skip to first unread message
Henry Story
Oct 29, 2017, 8:50:41 AM10/29/17
to HoTT Cafe
If my wife gives me a set of things to buy, eg. A = { sugar, flour, eggs, milk } and I come back with B = { wine, whiskey, cigars, newspaper } then both sets are isomorphic, but my wife won't be happy.
Why can't I invoke the Univalence Axiom in my defense to show that isomorphic things are identical?
---
I asked the above question on Stack Exchange Maths, but they immediately
put it on hold. Not much faith in themselves there.
https://math.stackexchange.com/questions/2494830/isomorphism-in-the-real-world
---
So my guess is that if I think semantically by thinking of the objects in the sets as
strings, and then we map those to objects in the real world using an interpretation function,
then indeed there is an function i1 to map A to objects in the real world that satisfy what
english speakers understand by the words in A, and there is another interpretation function i2
that maps the words of A to the way english speakers usually understand the words in B. So we assume that
because in the real world whiskey has all kinds of relations that flour does not have,
those two things are not exchangeable. In that case what is the case is that A is isomorphic to
B comes to saying one could have used the words in A to mean what the words in B mean and vice
versa, but once one settles on one interpretation function then there is a difference, because
the interpretation functions are different.
But then if A = B, can the interpretation function really be different?
Henry
Why can't I invoke the Univalence Axiom in my defense to show that isomorphic things are identical?
---
I asked the above question on Stack Exchange Maths, but they immediately
put it on hold. Not much faith in themselves there.
https://math.stackexchange.com/questions/2494830/isomorphism-in-the-real-world
---
So my guess is that if I think semantically by thinking of the objects in the sets as
strings, and then we map those to objects in the real world using an interpretation function,
then indeed there is an function i1 to map A to objects in the real world that satisfy what
english speakers understand by the words in A, and there is another interpretation function i2
that maps the words of A to the way english speakers usually understand the words in B. So we assume that
because in the real world whiskey has all kinds of relations that flour does not have,
those two things are not exchangeable. In that case what is the case is that A is isomorphic to
B comes to saying one could have used the words in A to mean what the words in B mean and vice
versa, but once one settles on one interpretation function then there is a difference, because
the interpretation functions are different.
But then if A = B, can the interpretation function really be different?
Henry
Siddhartha Gadgil
Oct 29, 2017, 9:04:11 AM10/29/17
to Henry Story, HoTT Cafe
They are isomorphic (hence equal) _as sets_, but not _as food_. Uni valence does not mean permission to us forgetful functors to sets.
regards,
Siddhartha
--
You received this message because you are subscribed to the Google Groups "HoTT Cafe" group.
To unsubscribe from this group and stop receiving emails from it, send an email to hott-cafe+...@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
Henry Story
Oct 29, 2017, 11:28:54 AM10/29/17
to Siddhartha Gadgil, HoTT Cafe
On 29 Oct 2017, at 14:03, Siddhartha Gadgil <siddhart...@gmail.com> wrote:They are isomorphic (hence equal) _as sets_, but not _as food_. Uni valence does not mean permission to us forgetful functors to sets.
Mhh with a bit of help I reframed the question into one that was more mathematical all round and got
this answer which seems reasonble to me:
"Univalence is about equivalence of types inhabiting a Universe, but {1,2,3} is not such a type, it is a term of a set inhabiting U."
Guillaume Brunerie
Oct 29, 2017, 12:51:47 PM10/29/17
to Henry Story, Siddhartha Gadgil, HoTT Cafe
Well, you can use univalence to prove that isomorphic groups are
equal, for instance, so it’s not just about elements of U. (A
consequence of) univalence says that if two structures are isomorphic
(for the right notion of isomorphism for these structures), then they
are equal.
The thing is that in order to apply univalence to deduce that two such
things are equal, you have to know what you are talking about : you
have to be very clear about the *type* of the objects you want to
apply univalence to.
For instance, you could ask the question: Is N equal to Z?
The answer to that question depends on what structure you are
(implicitely) considering N and Z to have. For instance if you
consider them as sets, or as pointed sets, they are equivalent (hence
equal), but if you consider them as monoids, they are not.
Another example: Is 2Z equal to Z?
If you consider them as groups, then yes. If you consider them as
subgroups of Z, then no. If you consider them as topological spaces,
then yes. If you consider them as metric spaces, then no.
The thing is that when a mathematician says "A is equivalent to B", it
is often up to the reader to figure out what A and B are considered
as, in order for the statement to be both true and useful. For
instance if someone talks about 2Z, they probably see it as a subgroup
of Z, because it does not make much sense to consider 2Z only as a
group (why not just take Z instead?), but they might as some point
mention that it is equivalent to Z as a group. If someone talks about
Z[i], maybe they mean the abstract ring of Gaussian integers, or maybe
they mean the subring of C, strictly speaking it’s not the same thing
and it will depend on the context (and it could very well go back and
forth between the two different interpretations, even in the same
sentence).
In your example of sup({1,2,3}) ≠ sup({4,5,6}), the reason is that you
can only apply the sup function to a *subset of an ordered set*, not
to an arbitrary type. Therefore in order to deduce that equality, you
would need {1,2,3} to be equivalent to {4,5,6} *as subsets of N*,
which is not the case, even though they are equivalent as sets.
So if your wife asks you to buy A = { sugar, flour, eggs, milk }, it
is likely that she did not consider A as simply a set which happens to
have four elements, but as a sets of things that are needed for a
specific purpose (cooking, for instance). You could still use some
form of "univalence". For instance if she asks you to buy white sugar
and you buy brown sugar, it might be fine depending on the intended
usage. If you buy brown eggs instead of white eggs, it’s most likely
ok (unless they are meant as decoration, maybe). If you buy margarine
instead of butter it might be ok. If you buy gluten-free flour instead
of all-purpose flour it might be fine or not, again depending on the
intended usage (for thickening sauces, both should work, but for
making cakes, less so). If you buy whiskey instead of ice-cream, it
might be fine if the intended purpose is to have some comfort food for
when you’re feeling down (and assuming both serve that purpose equally
well).
So your job, as the grocery-shopper, is to understand the (implicit)
intended purpose, in order to be able to know in what cases you can
consider two items to be equivalent. And it’s only when two items are
equivalents with respect to the intended usage that you can apply
univalence and substitute one for the other.
Guillaume
equal, for instance, so it’s not just about elements of U. (A
consequence of) univalence says that if two structures are isomorphic
(for the right notion of isomorphism for these structures), then they
are equal.
The thing is that in order to apply univalence to deduce that two such
things are equal, you have to know what you are talking about : you
have to be very clear about the *type* of the objects you want to
apply univalence to.
For instance, you could ask the question: Is N equal to Z?
The answer to that question depends on what structure you are
(implicitely) considering N and Z to have. For instance if you
consider them as sets, or as pointed sets, they are equivalent (hence
equal), but if you consider them as monoids, they are not.
Another example: Is 2Z equal to Z?
If you consider them as groups, then yes. If you consider them as
subgroups of Z, then no. If you consider them as topological spaces,
then yes. If you consider them as metric spaces, then no.
The thing is that when a mathematician says "A is equivalent to B", it
is often up to the reader to figure out what A and B are considered
as, in order for the statement to be both true and useful. For
instance if someone talks about 2Z, they probably see it as a subgroup
of Z, because it does not make much sense to consider 2Z only as a
group (why not just take Z instead?), but they might as some point
mention that it is equivalent to Z as a group. If someone talks about
Z[i], maybe they mean the abstract ring of Gaussian integers, or maybe
they mean the subring of C, strictly speaking it’s not the same thing
and it will depend on the context (and it could very well go back and
forth between the two different interpretations, even in the same
sentence).
In your example of sup({1,2,3}) ≠ sup({4,5,6}), the reason is that you
can only apply the sup function to a *subset of an ordered set*, not
to an arbitrary type. Therefore in order to deduce that equality, you
would need {1,2,3} to be equivalent to {4,5,6} *as subsets of N*,
which is not the case, even though they are equivalent as sets.
So if your wife asks you to buy A = { sugar, flour, eggs, milk }, it
is likely that she did not consider A as simply a set which happens to
have four elements, but as a sets of things that are needed for a
specific purpose (cooking, for instance). You could still use some
form of "univalence". For instance if she asks you to buy white sugar
and you buy brown sugar, it might be fine depending on the intended
usage. If you buy brown eggs instead of white eggs, it’s most likely
ok (unless they are meant as decoration, maybe). If you buy margarine
instead of butter it might be ok. If you buy gluten-free flour instead
of all-purpose flour it might be fine or not, again depending on the
intended usage (for thickening sauces, both should work, but for
making cakes, less so). If you buy whiskey instead of ice-cream, it
might be fine if the intended purpose is to have some comfort food for
when you’re feeling down (and assuming both serve that purpose equally
well).
So your job, as the grocery-shopper, is to understand the (implicit)
intended purpose, in order to be able to know in what cases you can
consider two items to be equivalent. And it’s only when two items are
equivalents with respect to the intended usage that you can apply
univalence and substitute one for the other.
Guillaume
Julian Michael
Oct 29, 2017, 6:30:36 PM10/29/17
to Guillaume Brunerie, Henry Story, Siddhartha Gadgil, HoTT Cafe
There's also the issue of how to represent natural language meaning here, which adds some degrees of freedom in how you interpret this question (and, joyously, adds to the variety of possible responses). Personally, I would argue that the type theoretic representation of the request has nothing to do with the four-element set—rather, it is a request for an element of the product type (Sugar * Flour * Eggs * Milk). The question then is whether you can show that this type is equivalent to (Wine * Whiskey * Cigars * Newspaper). Maybe it's more clear now why univalence shouldn't help you.
Univalence is a way of giving us a form of observational or structural equality on types, i.e., equality is determined by behavior. In mathematics, the behavior of a type can be completely characterized by the relatively small set of operations you can carry out on that type (from its inductive definition, etc.). But in the real world, abstractions like "sugar", "flour", "eggs", and "milk" have an extremely rich set of behaviors, characterized by all of the various things you can observe about the objects described by these abstractions, and all of the things you can do with them. For example, one behavior of milk is its Color, which we can identify as white, i.e., color(milk) =_{Color} white. So one of the requirements for an isomorphism between the two requests will be showing color(newspaper) =_{Color} white.
If your concern is cooking, you can likely get away with bringing objects whose purposes in cooking are the same, sure. But in general, there is a massive multitude of behaviors associated with each of these abstractions, all of which would have to be perfectly replicated in order for the equality to be carried out.
In fact, univalence once again proves more natural to have than not. Because suppose you brought an object that in every conceivable circumstance looked, behaved, tasted, etc. exactly like an egg would. But you insisted, no—this is not actually an egg, because it lacks some fundamental, primitive eggness that was impossible to observe in-and-of-itself. People would look at you like you were a continental philosopher (i.e., like you were completely out of your mind). Because at the end of the day our linguistic abstractions are defined by behaviors as well.
Henry Story
Oct 30, 2017, 8:20:43 AM10/30/17
to Julian John Michael, Guillaume Brunerie, Siddhartha Gadgil, HoTT Cafe
On 29 Oct 2017, at 23:30, Julian Michael <julianjo...@gmail.com> wrote:
There's also the issue of how to represent natural language meaning here, which adds some degrees of freedom in how you interpret this question (and, joyously, adds to the variety of possible responses). Personally, I would argue that the type theoretic representation of the request has nothing to do with the four-element set—rather, it is a request for an element of the product type (Sugar * Flour * Eggs * Milk). The question then is whether you can show that this type is equivalent to (Wine * Whiskey * Cigars * Newspaper). Maybe it's more clear now why univalence shouldn't help you.
Damn! ;-)
Univalence is a way of giving us a form of observational or structural equality on types, i.e., equality is determined by behavior. In mathematics, the behavior of a type can be completely characterized by the relatively small set of operations you can carry out on that type (from its inductive definition, etc.). But in the real world, abstractions like "sugar", "flour", "eggs", and "milk" have an extremely rich set of behaviors, characterized by all of the various things you can observe about the objects described by these abstractions, and all of the things you can do with them. For example, one behavior of milk is its Color, which we can identify as white, i.e., color(milk) =_{Color} white. So one of the requirements for an isomorphism between the two requests will be showing color(newspaper) =_{Color} white.
If your concern is cooking, you can likely get away with bringing objects whose purposes in cooking are the same, sure. But in general, there is a massive multitude of behaviors associated with each of these abstractions, all of which would have to be perfectly replicated in order for the equality to be carried out.
In fact, univalence once again proves more natural to have than not. Because suppose you brought an object that in every conceivable circumstance looked, behaved, tasted, etc. exactly like an egg would. But you insisted, no—this is not actually an egg, because it lacks some fundamental, primitive eggness that was impossible to observe in-and-of-itself. People would look at you like you were a continental philosopher (i.e., like you were completely out of your mind). Because at the end of the day our linguistic abstractions are defined by behaviors as well.
Yes, and I suppose if my wife who we'll say now is blind, told me to get an instance of
Sugar x Flour x Eggs x Milk
and I came back with
Milk x Sugar x Flour x Eggs x 1
Sugar x Flour x Eggs x Milk
and I came back with
Milk x Sugar x Flour x Eggs x 1
say because I have a box with 5 rows, and I filled the last row with air
then I could argue that the above structure is isomorphic
with the requested one, and so that we were just "looking" at the same abstract object from
The first question I asked a few years ago on this list asked
with the requested one, and so that we were just "looking" at the same abstract object from
different points of view, though of course being blind, it would be quite important to map
the location of the one to the other -- which I guess is the point of the talk of transporting
functions along the isomorphism that some of the detailed answers on StackExchange go into.
https://math.stackexchange.com/questions/2494960/a-basic-univalence-puzzle-concerning-the-sup-function-on-sets
Btw. your talk of observation made me think of the recently published book by Bart Jacobs
https://math.stackexchange.com/questions/2494960/a-basic-univalence-puzzle-concerning-the-sup-function-on-sets
Btw. your talk of observation made me think of the recently published book by Bart Jacobs
"Introduction to Coalgebra, Towards a Mathematics of States and Observation"
which I have been studying carefully, especially because I came across
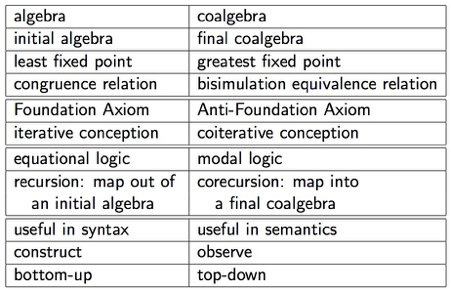
Corina Cirstea's paper "Modal Logics are Coalgebraic" [1] and
figures such as this [2] which show a quite a stunning symmetry.

The first question I asked a few years ago on this list asked
how HoTT tied in with modal logic, which I studied in great detail.
So I wonder how this algebra/co-algebra distinction turn up on HoTT.
I found the following blog post on co-inductive types and HoTT [3],
but have not yet studied it, as I am finishing up a report on the
semantic web and coalgebras.
We have been speaking about observation and semantics which ties words
to the real world, so it seems relevant. :-)
[2] which I found in a a deck probably presented by Lawrence S. Moss at the Mathlogaps 2008 workshop in Manchester in 2008 « Coalgebra and Circularity » https://www.cs.indiana.edu/cmcs/finitary.pdf
[3]
Julian Michael
Oct 30, 2017, 11:21:54 AM10/30/17
to Henry Story, Guillaume Brunerie, Siddhartha Gadgil, HoTT Cafe
For sure, coinduction is interesting and seems like it could be useful if we want to describe real-world objects, since they are in some sense defined by the observations we can make on them (and sometimes these observations may involve producing new objects of the same type) so equality by bisimulation seems appropriate. But also in the real world, physical objects generally occupy unique subsets of space and time, and entities are constructed through physical or mental processes, so it’s not clear to me that there is any use of their principles for construction/elimination in this case. Instead abstract data types (i.e., records or sigma types where the first element is in U) would be more appropriate. From an AI perspective, abstract data types are actually more useful since they afford you the ability to choose a type as the mental representation of an entity, and represent observations as explicit functions on this underlying representation.
That’s all I’ll say on that issue here, having gotten sufficiently off-topic... :)
That’s all I’ll say on that issue here, having gotten sufficiently off-topic... :)
Reply all
Reply to author
Forward
0 new messages
