简明因果判定方法
32 views
Skip to first unread message
Qing
Sep 24, 2008, 1:46:53 AM9/24/08
to tt...@googlegroups.com
分析问题一个重要的目的是为了寻求因果关系,关于如何找到这种关系,前人有所研究,虽然不是数量上,但从逻辑上,给出了几种方法。请看以前写的这篇文章:
http://groups.google.com/group/ttnn/browse_thread/thread/894381b227a1c8bd/4c53f0eb2661d279
非常严谨的因果关系是很难判断的,大多数情况下,我们其实并不一定真的是要找因果,而是要找到相关性,当两个因素存在相关性的时候,表面上是有些因果关系的(虽然也不一定存在)。比如奥运和灾害,看上去有些关联,如果在古代,迷信点的会很容易建立一种因果关系。但也可以这么说,是因为奥运需要媒体开放,而媒体开放导致关于灾害的事情多了起来,这可能是一种间接的因果。
寻找绝对的因果,那是物理定律,而在我们平常生活里面,一般都是要寻求一种解释。
我们可以建立数据挖掘模型来判断因果关系,一般来说,那个"果"是被当作目标变量的。但其实,一般的数据统计也能给出单个因素的影响,绝大多数情况下,我想这种粗浅的因果判定是足够的。因此,这里提出一种简明的寻求因素间因果关系的判别方法。
首先,如何表达 因-果。
对此,我想借用OLAP的表达形式,"因果"都可以用维度值来表示。果,体现在一个维度上面,表明了一种状态,而因呢,是其他各种维度,表明了其他的一些状态。再借用一个挖掘的术语,叫做观测。判断因果,是建立在对很多观测上,这些维度的值来观察得到的。
举个例子来说,比如我们要分析什么因素导致客户价值的波动。那么就对大量的客户观察,观察其价值波动、他的年龄、收入、通话结构变化等等因素。这些因素都成为维度,而度量,则是客户数。于是,形成了这样一个多维的视图:
(价值波动、年龄、收入、交往圈波动、客户数)
其中,价值波动这个维度就是要分析的"果",而因,则是要从年龄、收入、交往圈波动里面寻找。请注意,因为年龄、收入这些都是维度,因此,他们都是离散的值,需要一些处理,比如通过观察分布去离散化。
在用维度来表示因果,之后,来看看总体的判别因果的思路。这里没什么高深的算法,只是将我们人工的判断自动化而已。所以,先来说说人工如何来判断因果。还是用这个例子来说。
价值波动维度,称之为"果维度"吧,其中包含三个值 (上升、平稳、下降)。分析目标就是判断,年龄、收入、交往圈波动的不同维度值(称之为因维度吧)对这三种结果的影响。假设,年龄角度有五个值,18岁以下,18-25岁,...60岁以上,收入呢,有7个维度值,交往圈波动有扩大、缩小、基本稳定三个维度值。于是,就可以通过观察具备因维度值的客户群在果维度维度值的分布比例情况,如果这个分布跟所有客户在果维度维度值的分布一致,那么这个因维度值就不是一个影响因素,如果差异大,就是一个潜在的影响因素。这还是比较简单吧。
说的形象一点,用例子。假设全体客户在果维度的三个值的比例分别是(上升:20%,平稳:65%, 下降:15%),观察18岁以下这个因维度值是否是影响因素。就可以通过18岁以下的客户群在果维度的分布来判断,如果这个分布是(50%, 32%, 18%),可以看到他跟总体分布的"上升"值分布有显著的差异,增长了两倍。于是基本可以得出结论,年龄18岁以下对价值提升有促进作用,这就是一个因果结论。
上面介绍的是人工的判定方法,相信从这个步骤,大家可以看到要自动计算也不是什么难事。当然,要对"显著的差异"有个量化的定义标准才行,否则也要人工诸多判断。这个问题改天再说。
http://groups.google.com/group/ttnn/browse_thread/thread/894381b227a1c8bd/4c53f0eb2661d279
非常严谨的因果关系是很难判断的,大多数情况下,我们其实并不一定真的是要找因果,而是要找到相关性,当两个因素存在相关性的时候,表面上是有些因果关系的(虽然也不一定存在)。比如奥运和灾害,看上去有些关联,如果在古代,迷信点的会很容易建立一种因果关系。但也可以这么说,是因为奥运需要媒体开放,而媒体开放导致关于灾害的事情多了起来,这可能是一种间接的因果。
寻找绝对的因果,那是物理定律,而在我们平常生活里面,一般都是要寻求一种解释。
我们可以建立数据挖掘模型来判断因果关系,一般来说,那个"果"是被当作目标变量的。但其实,一般的数据统计也能给出单个因素的影响,绝大多数情况下,我想这种粗浅的因果判定是足够的。因此,这里提出一种简明的寻求因素间因果关系的判别方法。
首先,如何表达 因-果。
对此,我想借用OLAP的表达形式,"因果"都可以用维度值来表示。果,体现在一个维度上面,表明了一种状态,而因呢,是其他各种维度,表明了其他的一些状态。再借用一个挖掘的术语,叫做观测。判断因果,是建立在对很多观测上,这些维度的值来观察得到的。
举个例子来说,比如我们要分析什么因素导致客户价值的波动。那么就对大量的客户观察,观察其价值波动、他的年龄、收入、通话结构变化等等因素。这些因素都成为维度,而度量,则是客户数。于是,形成了这样一个多维的视图:
(价值波动、年龄、收入、交往圈波动、客户数)
其中,价值波动这个维度就是要分析的"果",而因,则是要从年龄、收入、交往圈波动里面寻找。请注意,因为年龄、收入这些都是维度,因此,他们都是离散的值,需要一些处理,比如通过观察分布去离散化。
在用维度来表示因果,之后,来看看总体的判别因果的思路。这里没什么高深的算法,只是将我们人工的判断自动化而已。所以,先来说说人工如何来判断因果。还是用这个例子来说。
价值波动维度,称之为"果维度"吧,其中包含三个值 (上升、平稳、下降)。分析目标就是判断,年龄、收入、交往圈波动的不同维度值(称之为因维度吧)对这三种结果的影响。假设,年龄角度有五个值,18岁以下,18-25岁,...60岁以上,收入呢,有7个维度值,交往圈波动有扩大、缩小、基本稳定三个维度值。于是,就可以通过观察具备因维度值的客户群在果维度维度值的分布比例情况,如果这个分布跟所有客户在果维度维度值的分布一致,那么这个因维度值就不是一个影响因素,如果差异大,就是一个潜在的影响因素。这还是比较简单吧。
说的形象一点,用例子。假设全体客户在果维度的三个值的比例分别是(上升:20%,平稳:65%, 下降:15%),观察18岁以下这个因维度值是否是影响因素。就可以通过18岁以下的客户群在果维度的分布来判断,如果这个分布是(50%, 32%, 18%),可以看到他跟总体分布的"上升"值分布有显著的差异,增长了两倍。于是基本可以得出结论,年龄18岁以下对价值提升有促进作用,这就是一个因果结论。
上面介绍的是人工的判定方法,相信从这个步骤,大家可以看到要自动计算也不是什么难事。当然,要对"显著的差异"有个量化的定义标准才行,否则也要人工诸多判断。这个问题改天再说。
Qing
Sep 26, 2008, 1:40:00 AM9/26/08
to tt...@googlegroups.com
前天介绍了这种简明因果判断方法的思路,借助olap的思想,区分因果维度,从度量在果维度上的分布比例差异来判断因果关系。
呃,虽然举了一些例子,但没图还是不容易理解,因此,这里再深入一下。稍稍形式化地表达,以期让这个方法看上去完整一些。再辅以图表,以期让他更易理解。
还得设想一个场景来说事,不过这次抛开太多的具体描述,都用符号来表示。于是问题是这样的:
在一个多维的视图中:(D1, D2,D3...Dn, M),其中D1是果维度,包含了若干维度值(V11..V1i),D2到Dn都是因维度,M是对观测数据的汇总值。
请问,在D2到Dn各维度的维度值中,哪些是对D1的取值是有影响的?
为了说明方便,假设D1的取值有三种情况,跟前面的例子一样,上升,平稳和下降。首先,我们可以得到所有观测在这三种情况的分布,可以这么表示:
(D1, %(M))
因此,这个分布可能是这样的:
D1, %(M)
上升,26.7%
平稳,43.5%
下降,29.9%
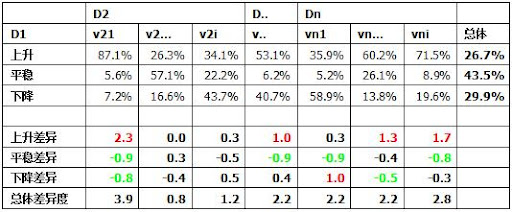
接着就是要看每个维度取值在D1三种情况的分布,并与总体分布进行对比,发现差异。如何表现这个差异呢?一开始,我尝试用这样一种方法,用"相对变化率"来表示,如图1(yinguo_1.jpg)所示:
针对D1的每个值,计算其他维度值的分布比例跟总体分布比例的差异,比如v21在上升情况的差异,就是(87.1%-26.7%)/26.7% = 2.3,这算一个很大的差异了。设定阈值,如果差异大于0.5,就是一个显著差异,红色标记。如果小于-0.5,也是一个显著差异,绿色标记。但我们首先观察的还不是每个具体差异值,而是要针对某个维度值的差异值进行绝对值相加,比如V21,最后的总体差异度就是3.9。
对总体差异度进行排序,就可以得出那些指标对D1的取值有显著影响,从上图看V21、Vni、是排在前头两个的。基本上是可以得出这种结论——"v21对上升有重要影响"。
而对于接下来的总体差异度均为2.2的,可以考虑一些细节,比如vn1的影响主要是导致下降情况,因为那里有个红色的1.0,而其他两个基本都有些对上升的促进作用。而对于0.8,1.2那两个,基本就可以忽略不计了,可以认为他们对上升或是下降没有影响。
如何定义显著差异的阈值呢?我现在还没有发现绝对的数值标准,也许正负0.5是可以的,但这个最好还是看排名情况,取差异值相对较大的应该更容易帮助解读。
另外还有个问题,在这个例子里面,总体分布里面,几种情况的分布比较适中,最少也是26.7%,但如果遇到一些极端的分布比例怎么办呢?比如一个80%,用这种相对变化率来表示,即便变化到从80%变化到20%,计算出来的差异值也很小。
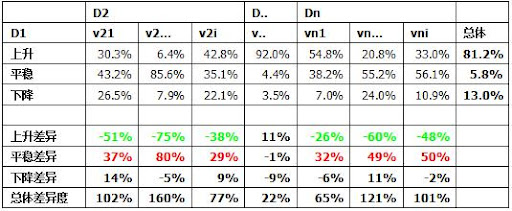
想想,还不如直接简单一些,就用比例差值来表示差异,如图2(yinguo_2.jpg):
某个因素的总体差异值,就是不同差异值的绝对值之和。这个值越大,就说明这个因素对结果影响最大。而判断具体差异值的大小和正负符号,还可以判断该因素究竟对哪一种结果有多大影响,而且影响是正向还是反向的。
这种方法也就是纯粹计算而已,没什么复杂的逻辑。如果普通的olap工具都具备这种分析功能就好了。
呃,虽然举了一些例子,但没图还是不容易理解,因此,这里再深入一下。稍稍形式化地表达,以期让这个方法看上去完整一些。再辅以图表,以期让他更易理解。
还得设想一个场景来说事,不过这次抛开太多的具体描述,都用符号来表示。于是问题是这样的:
在一个多维的视图中:(D1, D2,D3...Dn, M),其中D1是果维度,包含了若干维度值(V11..V1i),D2到Dn都是因维度,M是对观测数据的汇总值。
请问,在D2到Dn各维度的维度值中,哪些是对D1的取值是有影响的?
为了说明方便,假设D1的取值有三种情况,跟前面的例子一样,上升,平稳和下降。首先,我们可以得到所有观测在这三种情况的分布,可以这么表示:
(D1, %(M))
因此,这个分布可能是这样的:
D1, %(M)
上升,26.7%
平稳,43.5%
下降,29.9%
接着就是要看每个维度取值在D1三种情况的分布,并与总体分布进行对比,发现差异。如何表现这个差异呢?一开始,我尝试用这样一种方法,用"相对变化率"来表示,如图1(yinguo_1.jpg)所示:
针对D1的每个值,计算其他维度值的分布比例跟总体分布比例的差异,比如v21在上升情况的差异,就是(87.1%-26.7%)/26.7% = 2.3,这算一个很大的差异了。设定阈值,如果差异大于0.5,就是一个显著差异,红色标记。如果小于-0.5,也是一个显著差异,绿色标记。但我们首先观察的还不是每个具体差异值,而是要针对某个维度值的差异值进行绝对值相加,比如V21,最后的总体差异度就是3.9。
对总体差异度进行排序,就可以得出那些指标对D1的取值有显著影响,从上图看V21、Vni、是排在前头两个的。基本上是可以得出这种结论——"v21对上升有重要影响"。
而对于接下来的总体差异度均为2.2的,可以考虑一些细节,比如vn1的影响主要是导致下降情况,因为那里有个红色的1.0,而其他两个基本都有些对上升的促进作用。而对于0.8,1.2那两个,基本就可以忽略不计了,可以认为他们对上升或是下降没有影响。
如何定义显著差异的阈值呢?我现在还没有发现绝对的数值标准,也许正负0.5是可以的,但这个最好还是看排名情况,取差异值相对较大的应该更容易帮助解读。
另外还有个问题,在这个例子里面,总体分布里面,几种情况的分布比较适中,最少也是26.7%,但如果遇到一些极端的分布比例怎么办呢?比如一个80%,用这种相对变化率来表示,即便变化到从80%变化到20%,计算出来的差异值也很小。
想想,还不如直接简单一些,就用比例差值来表示差异,如图2(yinguo_2.jpg):
某个因素的总体差异值,就是不同差异值的绝对值之和。这个值越大,就说明这个因素对结果影响最大。而判断具体差异值的大小和正负符号,还可以判断该因素究竟对哪一种结果有多大影响,而且影响是正向还是反向的。
这种方法也就是纯粹计算而已,没什么复杂的逻辑。如果普通的olap工具都具备这种分析功能就好了。
Qing
Oct 14, 2008, 2:00:32 AM10/14/08
to tt...@googlegroups.com
先抱个歉。因为,在上次探讨这个因果判断方法的时候,弄错了。那两个图片中的百分比是我用excel的随机数生成,只考虑了在果维度上分布百分比加起来等于百分百,但没有考虑他跟总体百分比的逻辑关系。
因此,上面这两个图片中,"总体"一栏的数字是不存在的。而原来设想的"总体差异度",通过它来判断哪个因维度影响最大,也是不可能的,因为每个总体差异度肯定是等于0。
不用真实的数据来验证还真的发现不了问题,上周我正用这个方法来分析因果,才暴露出来。
所以,这里要澄清一下。另外,这这次分析中,发现还可以进行一些优化。观察果维度分布差异的方法还是不变。但后来发现,这种差异跟每个维度分布的观察数有关系,观测数越多,差异越小。观测数少,差异就可能被放大。因此,要消除这种因为观测数的影响。
这次,我准备用真实的数据,只是隐藏因和果的描述。如下图:
左上表,为某个因维度跟果维度的交叉分布表,左下表是因维度与果维度的分布差异。右变两个图,是根据左下表作出的可视化图形。
分布差异表,为每个因维度值上,果维度的分布减去果维度的总体分布,再乘以该因维度值占总体值得分布。
于是,比如因1和果2的差异值=(4054/14799-561200/1266912)*14799/1266912)
而从分布差异表看,横向和纵向的百分比之和都为0。这表示,因维度造成的结果,只是在一个群体里面此消彼长。(如果某个原因可能造成多种结果,这个矩阵可能不太适合。因此,需要明确业务问题,结果的几个现象应当是非此即彼的)
看右上图,可以更直观一点看这个差异表。此图应当这么看,在正向y轴的柱子,表示了某种因对某种果有促进作用。而且,柱子越长,作用越大。比如因4的红色柱子,因为红色表示果3,相比其他,没有谁的红色柱子比他长,因此可以说,因4对果3有很大的作用。当然,是否这是一个最大的因素呢?还需要看其他的因维度。但这里的差异百分比已经比较,这里的差异是2.4%,如果有另一个因维度值在果3的差异是2.5%,可以认为那是一个更大的因素。
或者换个角度,如右下图,可以看到究竟这个因维度对三种不同结果的综合影响,可以根据柱子上下的跨度对比来判断。
在列出每个因维度对果维度的差异之后,可以对差异值进行排序,如此,就可以解读出来,导致某个结果的主要因素为哪一些。
因此,上面这两个图片中,"总体"一栏的数字是不存在的。而原来设想的"总体差异度",通过它来判断哪个因维度影响最大,也是不可能的,因为每个总体差异度肯定是等于0。
不用真实的数据来验证还真的发现不了问题,上周我正用这个方法来分析因果,才暴露出来。
所以,这里要澄清一下。另外,这这次分析中,发现还可以进行一些优化。观察果维度分布差异的方法还是不变。但后来发现,这种差异跟每个维度分布的观察数有关系,观测数越多,差异越小。观测数少,差异就可能被放大。因此,要消除这种因为观测数的影响。
这次,我准备用真实的数据,只是隐藏因和果的描述。如下图:
左上表,为某个因维度跟果维度的交叉分布表,左下表是因维度与果维度的分布差异。右变两个图,是根据左下表作出的可视化图形。
分布差异表,为每个因维度值上,果维度的分布减去果维度的总体分布,再乘以该因维度值占总体值得分布。
于是,比如因1和果2的差异值=(4054/14799-561200/1266912)*14799/1266912)
而从分布差异表看,横向和纵向的百分比之和都为0。这表示,因维度造成的结果,只是在一个群体里面此消彼长。(如果某个原因可能造成多种结果,这个矩阵可能不太适合。因此,需要明确业务问题,结果的几个现象应当是非此即彼的)
看右上图,可以更直观一点看这个差异表。此图应当这么看,在正向y轴的柱子,表示了某种因对某种果有促进作用。而且,柱子越长,作用越大。比如因4的红色柱子,因为红色表示果3,相比其他,没有谁的红色柱子比他长,因此可以说,因4对果3有很大的作用。当然,是否这是一个最大的因素呢?还需要看其他的因维度。但这里的差异百分比已经比较,这里的差异是2.4%,如果有另一个因维度值在果3的差异是2.5%,可以认为那是一个更大的因素。
或者换个角度,如右下图,可以看到究竟这个因维度对三种不同结果的综合影响,可以根据柱子上下的跨度对比来判断。
在列出每个因维度对果维度的差异之后,可以对差异值进行排序,如此,就可以解读出来,导致某个结果的主要因素为哪一些。
Reply all
Reply to author
Forward
0 new messages