A sequel to my 1996 "ultimate ensemble theory" paper
Max
After a decade of procrastination, I've finally finished writing up a
sequel to that paper that I wrote back in 1996 (Is "the theory of
everything'' merely the ultimate ensemble theory?) that's been the
subject of so much interesting discussion in this group.
It's entitled "The Mathematical Universe", and you'll find it at
http://arxiv.org/pdf/0704.0646 and http://space.mit.edu/home/tegmark/toe.html
- I'd very much appreciate any comments that you may have.
The purpose of this paper is both to clarify what I mean by the Level
IV Multiverse and to further explore various implications, so it has
lots of discussion of stuff like the simulation argument, the relation
to Schmidhuber's ideas, Gödel incompleteness and Church-Turing
incomputability. Please let me apologize in advance for the fact that
Sections III, IV and the appendix of this paper are quite technical,
so if you're among the 99.99% who don't have a Ph.D. in theoretical
physics, perhaps skip those sections. I've added links to more
accessible papers touching on some of these issues at
http://space.mit.edu/home/tegmark/toe.html, and I'll try to write
something less obtuse soon.
Finally, if you discover a good time stretching device, please let me
know! Although I'm embarrassed that I haven't found the time to follow
and participate in the fascinating discussions in this group, the fact
that there's such interest has inspired and motivated me to continue
pursuing these ideas despite the discouragement from mainstream
academia. So thanks for the encouragement!
Max
;-)
Bruno Marchal
Le 11-avr.-07, à 17:25, Max a écrit :
>
> Hi Folks,
Hi Max, Nice you remember us.
>
> After a decade of procrastination, I've finally finished writing up a
> sequel to that paper that I wrote back in 1996 (Is "the theory of
> everything'' merely the ultimate ensemble theory?) that's been the
> subject of so much interesting discussion in this group.
Are you aware of the critics I have made about it, and about
Schmidhuber approach? I am not sure you have taken those critics into
account in your new paper, although on some point it is indeed clearer.
Oh, I see you are mistaken about Godel's theorem (hope you don't mind
the typical frankness in our discussion, mainly for reason of being
short). Perhaps this will be an opportunity to have a straight
discussion, and to help the go beyond the usual gap between logicians,
which in my opinion have developed the right tools, and the physicists,
which in general have kept the right (scientific realist) motivations.
> It's entitled "The Mathematical Universe", and you'll find it at
> http://arxiv.org/pdf/0704.0646 and
> http://space.mit.edu/home/tegmark/toe.html
> - I'd very much appreciate any comments that you may have.
I will.
>
> The purpose of this paper is both to clarify what I mean by the Level
> IV Multiverse and to further explore various implications, so it has
> lots of discussion of stuff like the simulation argument, the relation
> to Schmidhuber's ideas, Gödel incompleteness and Church-Turing
> incomputability.
Schmidhuber leaves the list more than 5 years ago without answering
questions adressed to him. I hope you will be more serious. Apparently
you are not aware of my works, which I have explained more than once in
this list, and has been the subject of my PhD thesis in France a long
time ago (and this 20 years after having published the results). It is
not entirely your fault because I have not yet send my papers to the
arXiv.org or international journal. I don't submit more than one paper
every 500 years (g), and you are lucky because I have just do this
recently and my paper has been accepted for the cie 2007:
http://www.amsta.leeds.ac.uk/~pmt6sbc/cie07.html (nice if you could
come, but it is high level logic).
All my other papers was ordered by kind people with serious motivation
in my results or my approach (similar to ideas discussed in this list,
and indeed close (but quite different) of yours. You can find most of
those papers in my url below. Alas it does not contain my last two
papers (for copyright reason). One of the main result is that "if I am
a machine" then the observable universe cannot be described by a
machine: the laws of physics have to emerge from the math of cognition
(not of human cognition but of universal machine introspection). The
other result is a "direct" partial extraction of the physical laws by
the interview of an ideally self-referentially correct universal
machine, and evidences adds up that indeed there is a quantum computer
exploitable in "real time" in the neighborhood of almost all classical
universal machines. This shows there is plausibly a mathematical
justification of the qubits from the bits. So the
Everett-Graham-Deutsch-Zurek qubit from bit transformation admits a
reciprocal. This is going in your direction (classical platonist
mathematicalism), but like with Penrose, the reasons differ.
> Please let me apologize in advance for the fact that
> Sections III, IV and the appendix of this paper are quite technical,
> so if you're among the 99.99% who don't have a Ph.D. in theoretical
> physics, perhaps skip those sections. I've added links to more
> accessible papers touching on some of these issues at
> http://space.mit.edu/home/tegmark/toe.html, and I'll try to write
> something less obtuse soon.
>
> Finally, if you discover a good time stretching device, please let me
> know! Although I'm embarrassed that I haven't found the time to follow
> and participate in the fascinating discussions in this group, the fact
> that there's such interest has inspired and motivated me to continue
> pursuing these ideas despite the discouragement from mainstream
> academia. So thanks for the encouragement!
Thanks to you, Max. I appreciate very much your effort to explain
Everett. I really love your paper with Wheeler. And I appreciate you
have the courage you show in tackling very difficult questions which
are indeed a little bit out of the mainstream fashion. I have myself
got trouble after publishing the quantum suicide in 1988, like I got
problem in the seventies with the more general "computationist
suicide". You can consider my work as a generalisation of Everett's
(but see also Otto Rossler's endophysics) embedding of the subject (the
physicist) in the physical world (quantum mechanics), indeed I embed
the mathematician in arithmetic; or you can see it as a detailed
reconstruction of Penrose's argument, with similar conclusions
(although Penrose is deadly wrong on Godel). In my Siena paper, I show
that the interview of the self-referentially correct machine (I call
them Lobian in my thesis, papers and in this list) provides a cute,
transparent, purely arithmetical (but empirically testable),
interpretation of Plotinus's theology (including is Plato-Aristotelian
theory of matter: it is this one which makes the theory testable). This
shows also that once we assume the computationalist hypothesis (in the
form "I am a machine", not in the form the physical universe is a
machine), the theory of everything, whatever it is, splits into a
scientifically communicable part, and a scientifically not communicable
part, and this shows Plotinus is right in his critics of Aristotelian
theology. To be sure the machine does address some similar critics to
Plotinus.
Unfortunately I don't have find a way for stretching time, and I am
myself a bit busy. I will read your sequel at ease, and let you know my
comments. Hope you will be able to stretch time a bit by yourself so
that we will be able to discuss and clarify possible misunderstandings.
In the meantime you can read both the Universal Dovetailer Argument,
and an introduction to the Lobian interview in my paper:
http://iridia.ulb.ac.be/~marchal/publications/
SANE2004MARCHALAbstract.html
Best regards,
Bruno
Torgny Tholerus
> Hi Folks,
>
> After a decade of procrastination, I've finally finished writing up a
> sequel to that paper that I wrote back in 1996 (Is "the theory of
> everything'' merely the ultimate ensemble theory?) that's been the
> subject of so much interesting discussion in this group.
> It's entitled "The Mathematical Universe", and you'll find it at
> http://arxiv.org/pdf/0704.0646 and http://space.mit.edu/home/tegmark/toe.html
> - I'd very much appreciate any comments that you may have.
>
good. I agree with everything you write there. I found the CUH
(Computable Universe Hypothesis) very good, and most interesting was VII
G 2 (Abandoning the continuum altogether), that is exactly what I
believe in.
One problem I have not yet solved, is how to get all directions isomorph
if you have a discrete space-time. Maybe someone on this this list can
help me solve that problem?
Max, a suggestion to you is to skip the concept of "infinity" totally.
Your reasoning will be true even if you have a finite, but enough big,
universe. You don't need the infinity.
--
Torgny Tholerus
Bruno Marchal
I will first comment what you say about Gödel's theorem.
You say (pp 19, 20) that Gödel's second incompleteness theorem implies
that we can never be 100% sure that "this" (Peano Arithmetic, real
numbers, ...) is consistent, and that this would leave open the
possibility that a finite length proof of "0 = 1".
This is a very common misconception of Godel's incompleteness,
sometimes advocated by "relativists".
By "common" I mean that most good popularizations of Godel's results
address correctly this misconception. I am mainly thinking about
Smullyan's many books on this subject, or the more recent, quite
excellent, book by Torkel Franzèn "Gödel's Theorem An incomplete Guide
to its Use and Abuse". I certainly recommand it to anyone interested
in this list subject. Franzèn is a little weak on the *Use* of Gödel's
theorem, but quite excellent on the so widespread *Misuses* and
*Abuses*.
It is hard for me to believe you are serious on Gödel. Even if we grant
some possibility of doubting the consistency of Peano Arithmetic PA
(say) I don't see how you derive from Gödel's second theorem the
possibility of a finite proof of 0=1. Gödel's theorem is itself
provable in PA, so your doubt would have a circular origin. Would PA
proves its consistency, this could be doubtful too: after all, all
inconsistent theories do proof their own consistency. Then it is easy
to provide everyday informal quite convincing proof of the consistency
of PA by using the fact that the axioms of PA are satisfied by the
model (N, +, *), and the inference rule of PA are truth preserving).
Formally, the consistency of PA can be proved in weak fragment of ZF
(Zermelo Fraenkel set theory) by transfinite induction up to the little
constructive ordinal epsilon zero (Gentzen theorem).
Now, what is curious and amazing, is the following consequence of the
second incompleteness theorem: given that PA is consistent, but cannot
prove its consistency, it follows that the theory PA + [PA is
inconsistent], that is PA with the addition of the axiom Bf (beweisbar
false = false is provable) has to be consistent too! (why? because if
you can derive a contradiction in PA from Bf, you would prove in PA
that Bf -> f, that is ~Bf = PA's consistency, contradicting the second
incompleteness theorem. NOW, by Godel's COMPLETENESS (not
INcompleteness) theorem, all first order theory is consistent if and
only if the theory has a model (in the logician sense, that is a model
is a mathematical structure satisfying the axioms. I think your
misconception could come from this fact. Indeed the completeness
theorem entails that the theory PA+Bf , being con,sistent by Godel II,
has a model! So there is a mathematical structure which satisfies the
axiom of PA + there is a proof of a falsity. But PA can prove (like
weaker theories) that 0 is not (a godel number coding) a proof of f,
and that 1 is not a proof of f, and that 2 is not a proof of f, etc.
That is, for each natural number n, PA can prove that n is not the
godel number of a falsity f. Thus, in the model of PA+Bf, the object
corresponding to a proof of a falsity has to be different from any
natural number. logician describes such object has an infinite non
standard numbers, and it can't correspond to anything looking like a
finite proof of f, or 0=1.
By the way, this list mixes people with diploma and without, you could
have asked or participate, but then this is what you are doing now,
isn't it? I have a phd in logic and computer science, although my
motivation has always been biology and/or theology, I mean fundamental
questioning. People without diploma are often better on new or very old
questions because they are less prejudiced by granting less theories.
It is also why I like to interview directly universal machines.
What is much more annoying in your paper, and shows that you have never
really consulted this mailing list, is that you are still burying
under the rug the mind body problem, or the first person/third person
relation problem. Your use of the frog/bird distinction illustrates
that you are using implicitly, despite your mathematicalism which I
appreciate, some "mind-matter"-like identity theory capable of giving
sense to the notion of a physical structure and of an observer
belonging to it. This *can* make sense, but, especially with the
computationalist hypothesis (= I am turing emulable), such a thing has
to be justified. This follows from the Universal Dovetailer Argument +
the Movie-graph Argument. I have already show that the
computationalist hypothesis (roughly: there is a level of description
where I am Turing emulable) entails the falsity of the computational
universe thesis. Physicalness, with comp, is a global internal feature
of arithmetical reality emerging from "machine's dream gluing", to be
short.
Another problem, is that, although I agree with mathematicalism, I have
no clue of what could be "All Mathematics". But with the Church Thesis,
or Church-Turing thesis, it can be argued that arithmetical reality is
enough (even for set-theoretical talking machine). Analysis and
everyday informal mathematics can be justified from inside too. See my
other posts or my work (hmm...I should update my webpage with my last
papers). About some of your point on mathematics, I think category
theory could help you, but note that it will not help for defining the
whole of math.
I finish by saying that I am ok with your ERH (there exists an external
physical reality completely independent of us human).
But I do not believe there could exist a corresponding external
physical reality completely independent of us lobian entity, once we
assume the comp hyp, or even very weak version of the comp hyp). CF the
UDA reasoning.
About the MUH (Our external physical reality is a mathematical
structure), I find this very vague and ambiguous and have to think more
about how you derive it. With comp the physical has to emerge from a
notion of first person plural sharable experiences. Of course I am not
saying that comp is true, but I have made that first person sharable
experience enough precise so that it can be empirically tested, and I
can already show that many feature of quantum mechanics are
consequences of it. I hope to derive the local exploitability of
universal quantum machine in the neighborhood of (almost all) classical
universal, in the years to come, or to refute it, and thus refute the
comp hyp.
I show also that Godel's results (and Löb Solovay generalizations, ref
in my Lille thesis) provide a transparent arithmetical interpretation
of Plotinus theology, including his platonist theory of matter. The
UDA, then, can relate Plotinus with the comp hyp, and does illustrate
new relationships between Pythagorean and Platonist "theologies" (in
the greek sense, not necessarily in the Christian sense). See some
"theological" threads in the archive.
Bruno
Le 11-avr.-07, à 17:25, Max a écrit :
>
Jayceetout
In line with my preoccupation and passion: consciousness......... I
confine my comments to that narrow scope and offer the following
observations (which I did with my phenomenal consciousness! :-)
Page 4 Section D.
I cannot utter a 'WOOHOO!' too loud here, to finally see these kinds
of words appearing. There is a long record on this forum of me trying
to get people to _really_ grasp the nature of the difference between
"Description/Appearance(apparent causal necessity)/Phenomenon" to
"Explanation/Actual Causal Necessity/Noumenon". In Max's work we
clearly have the arrival of a scientifically valid noumenon.
You may be aware that I have been raving on ad nauseum here recently
about my "EC", which literally is a 'MUH'. The universe literally 'is'
an instantated EC, say MUHcol. We humans are literally an ongoing
proof written in EC.....albeit of a different nature to the one
proposed, say MUHmax. The difference between MUHmax and MUHcol are not
important - the fact of the clear appreciation and expression of the
ontological/epistemological 'cut' (as Howard Pattee[2] puts it) and
distinction is what is important. ..........the words clearly
distinguish 'being' from 'appearance'. They embed the origins of all
knowledge as sourced subjectively from within it....through the
embedded agency of the FROG scientist's depiction of the BIRD side of
the cut.
More than that, the words emerge in a way that is hard to argue
against without appearing (at least methodologically/virtually) to
hold rather bizarre views about the ontology (underlying reality) of
the universe - ...far more bizarre than any MUH.........as the final
para clearly shows. so ............YES!
RE: Frogs and Birds
Having said the above, I detect a possible small crack in the Bird/
Frog depiction that might open up a door for unfounded criticism
from those who struggle to see the difference between a noumenon and
phenomenon. What you are describing is what I have written about
(rather badly!) [1]: It is a 'dual aspect science'. What I described
there is the phenomenon aspect (T = FROG) and the 'noumenon' aspect
(T' = BIRD). Both are completely equivalent descriptions of the same
thing, the universe U(.) as T' and how that universe appears (T') when
you are made of it, inside it, with observational capacities delivered
by T', _not_ T. The 'helicopter/bird' view metaphor is not quite
right, IMO - the MUH is a noumenon and not to be confused with an
'objective view' (there is no such thing!)...the BIRD metaphor might
confuse things.
The missing subtlety, which undermines all empirical support for
MUHmax, is that both the FROG's view _AND_ the BIRD's view are
equally supported by any and all empirical work. (with specific ref to
the isomorphism sentence on P4, section D). The FROG can lay no claim
to exclusive use of empirical work - for the noumenon is the thing
that is actually generating the 'observation' intrinsic in ...as you
say on P4, top.....'processes that give rise to the familiar
sensations of self awareness' ......that the FROG has... that are the
single, mandated and only sources of all scientific evidence (where
scientist = FROG, and everything about the MUH is a product of that
perspective). Without that faculty there is no science.
I hope I am making sense here....I don't think you have made enough
mileage out of this brute FROG/BIRD reality as regards their place as
equals in provision of DESCRIPTION/EXPLANATION resp. using the same
evidence system: phenomenal consciousness.
RE: Final Note
There is one aspect to MUH which remains completely absent and which,
IMO, is absolutely vital to any real 'TOE'..... Whilst recognizing
that 'it is like something' to be FROG.....MUHmax provides no basis
for the necessity that it be 'like something' to be FROG under the
circumstances of being configured as a FROG. That 'contents of
consciousness/that which is seen/observed', is the single source of
all scientific evidence used in support of all FROG and BIRD MUH rule
sets (=FROG/BIRD aspect science)....Fine...But nowhere is the paper
MUHmax explanatory of how the BIRD view/descriptions provide the
phenomenal consciousness that the FROG uses to do observation in
support of all propositions for either collection of rules. After
all.....it is not the FROGs descriptions, derived _directly using_
observation of MUH that deliver the observations.........this is
oxymoronic.....rather it is the noumenon (The BIRD rules of MUHmax)
that delivers observation (the faculty of observation, through which
all FROG views are delivered).
A TOE must deliver 'everything', right? Well this chunk of
'everything' is not in the paper. None of the QM or anything else in
your paper does it, nor does it propose a principle upon which it may
be delivered....AFAICT. Maybe I missed it or have wires
crossed....Having said that, I don't believe you actually have to
deliver it right now............what is more important is mere
recognition of the need and a clear delineation of the responsibility
for the ultimate source of the FROG's ability to observe as BIRD-
aspect rules, not FROG-aspect rules.
To me the detail of the MUHmax is a side issue to the real message of
your paper......regardless of the chosen MUH (there could be 100
flavours including a MUHbruno and so on....), what has to happen to
science is that it must go 'dual aspect' and recognise KANT's error
that the noumenon is scientifically intractable........and that is,
in effect, what you have done...IMHO...of course....
I hope this is of some use..........
cheers
colin hales
[1] Hales, C. 'AI and Science's Lost Realm', IEEE Intelligent
Systems vol. 21, no. 3, 2006. 76-81.
[2] Pattee, H. H. 'The physics of symbols: bridging the epistemic
cut', Biosystems vol. 60, no. 1-3, 2001. 5-21.
marc....@gmail.com
knowledge far greater than mine!
Can't comment much on the technical stuff, but can talk about the
ontological assumptions. The trouble with Platonism is that it's far
too simplistic. *all* mathematical concepts are lumped into the same
category, which are then defined to exist objectively. Of course,
those who think mathematics is only a human invention (nominalists)
make exactly the same mistake as the Platonists. They lump *all*
mathematical concepts together, then define the lump to be a social
construct.
But before one starts talking about mathematical concepts, one must be
careful to distinguish between *kinds* of mathematical concepts. I
think that *some* mathematical concepts exist objectively, some
don't. I think we need to be careful to distinguish between
*Cognitive Models* (which make references to *mathematical objects*
which really do objectively) and *Cognitive Tools* (which include
*mathematical procedures* for reasoning about reality). So the
distinction here is between *mathematical objects* and *mathematical
cognitive tools*.
We need to remember that if all the universe is math, intelligent
observers have to *use* math to learn about math. The way observers
use math *internally* to reason about mathematical things *externally*
leads to the division between *mathematical cognitive tools*
(subjective) and *mathematical objects* (objective). Thus if all the
universe is math then I think we need to give up the idea of complete
objectivity. The *mathematical objects* are objectively real, the
*mathematical cognitive tools* aren't. However there is close
relationship between the mathematical objects and the *mathematical
cognitive tools*
Let me give you an example of what I mean, because I think you were
definitely on the right track when you were talking about the
relationship between formal systems and computational models.
Using my terminology, I think the formal systems are the objectively
existing *mathematical objects*, the computational models are
subjective *mathematical cognitive tools*. The computational model
is not a mathematical *thing* , it's a mathematical *procedure* that
observers use internally. Therefore, the computational model is not
something objectively real. However, there is a close mapping between
computational models and formal systems. This is hard to explain, but
let me say that I think that the *formal system* is the more general
concept. The computational model is a sort of *a subjective snap-
shot* of the formal system. An apt analogy here might be the taking
of photos - you can photograph a physical object from many different
angles. In my analogy, the formal system is the externally real
object being photographed, the computational model is the subjective
'photo' of the formal system.
Another example might be the relationship between Algebra and Category
Theory. Here I think standard Algebra is a tool-kit of (non-
objective) mathematical *procedures* and therefore not objectively
real. However, there is a mapping between standard Algebra and a more
general theory: Category Theory. The concepts in Category Theory
*are* I think objectively real (they are mathematical *objects*).
For instance, the algebraic *operation* '2+2' does not correspond to
anything objectively real. However the *category* - the number 4 -
*is* objectively real - because it's not a procedure, it's a
mathematical object. You see what I'm getting at?
In general, each *mathematical object* maps to a corresponding
*mathematical procedure*. The mathematical objects are objectively
real general concepts, the mathematical procedures are the subjective
internal snap-shots. What we need to remember, according to my
suppositions, is that mathematical concepts which represent *objects*
are objectively real, but mathematical concepts which represent
*procedures* aren't.
What all this is leading to is this punch-line: I
f we believe your 2nd postulate that all the universe is math(which I
do) I think we need to give up your first postulate. I do not see
what is so bad about giving up the idea ofa completely objective
description of reality. I do not believe that giving up the
objectivity postulate would spell the end of the quest for a TOE. It
would just mean that a TOE would have to *include* direct conscious
experience (subjective elements) in order to be fully comprehended.
This sounds highly strange, but it's not impossible.
Onward! Cheers!
marc....@gmail.com
connecting three mathematical concepts: Formal Systems, Mathematical
Structures and Computations. I think you're definitely on to something
big with that intriguing diagram but you need to get it exactly right.
I don't believe that this is a complete classification of mathematical
concepts. What is missing are the concepts from probability theory:
things like Probability Distributions. Also (as I pointed out in my
last post), the term 'Mathematical Structures' should really be spit
in two: you could distinguish between specific Algebraic structures
and the most general structures from Category Theory. My own diagram
has SIX of those circles.
You've made some intriguing preliminary attempts to show the
relationships between the various mathematical concepts but I don't
think you've got them right yet. For instance (as I mentioned) I
think computations are special cases of formal systems. (*not*, as
you have in your diagram, special cases of mathematical structures).
I would be particualrly interested to hear what Bruno has to say about
that diagram and the nature of the relationship between the various
mathematical concepts.
Torgny Tholerus
Hi Folks, After a decade of procrastination, I've finally finished writing up a sequel to that paper that I wrote back in 1996 (Is "the theory of everything'' merely the ultimate ensemble theory?) that's been the subject of so much interesting discussion in this group. It's entitled "The Mathematical Universe", and you'll find it at http://arxiv.org/pdf/0704.0646 and http://space.mit.edu/home/tegmark/toe.html - I'd very much appreciate any comments that you may have.

But there is a length scale "1" of special significance in our physical space, namely the Planck length:
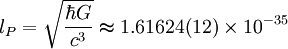 meter.
And there is a time period of special significance, namely the Planck
time:
meter.
And there is a time period of special significance, namely the Planck
time:
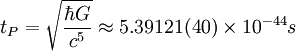 .
(Source: Wikipedia.)
.
(Source: Wikipedia.)
- --
- Torgny Tholerus
marc....@gmail.com
You may be interested in checking out the top-level 'Class Diagram of
Reality' which I just posted. It gives a graphical representation of
my ideas about ontology. The Mathematical concepts are all on the
right-hand side of the page and you can see from the diagram that I
think there are 9 fundamental areas of mathematical knowledge.
Incidentally the so-called 'Theory of Everything' pursued by main-
stream physics would fit entirely into the 3 boxes at the bottom left
of my diagram ;)
Link:
http://marc.geddes.googlepages.com/MCRT_ClassDiagram.html
William
I'm writing down my first thoughts, I was surprised you used the "free
of baggage" argument to argue that ERH ==> MUH, I would rather have
thought of a simulation kind of argument here but nevertheless,
interesting.
Also, since there's no observational difference between ERH and a
Copenhagen interpretation of ERH, I do not see any kind of conflict
there either ?
Also, one big question I have after reading your paper, what is the
TOE or what would you consider to be the TOE ?
I guess it would be the initial conditions and everything which
influences our universe (even if we can not observe it ourselves).
Because in some way, the simple statement that everything mathematical
is also physical, is already a TOE as it explains everything.
Finally, if anyone would have a rigorous proof that the existence of
mathematics implies human existence (which I believe must be
possible), I would be very interested to hear that.
Max
comments on this paper.
I hope to respond to them once teaching finishes and I (hopefully)
come up for air later this month.
In the mean time, I'd like to alert you to http://www.fqxi.org/community/index.php
If you're interested, you'll be able to apply for research grants here
next year to think about the sort of big questions discussed on this
list, regardless of your nationality and whether you're in academia or
not.
Moreover, you're welcome to participate in the discussion forum that
was just launched today at http://www.fqxi.org/community/forum.php, so
please consider copying stuff you post to this list to the Ultimate
Reality section there.
This has the advantage of getting your ideas out to lots of unusually
open-minded scientists (see http://www.fqxi.org/members.html).
Cheers,
Max
;-)
Bruno Marchal
Le 08-mai-07, à 05:13, Max a écrit :
>
> Thanks to all of you who have posted/sent interesting and helpful
> comments on this paper.
You are welcome.
> I hope to respond to them once teaching finishes and I (hopefully)
> come up for air later this month.
Take it easy. I will myself try to sum up in some non technical way
what I try to convey in the list.
>
> In the mean time, I'd like to alert you to
> http://www.fqxi.org/community/index.php
> If you're interested, you'll be able to apply for research grants here
> next year to think about the sort of big questions discussed on this
> list, regardless of your nationality and whether you're in academia or
> not.
> Moreover, you're welcome to participate in the discussion forum that
> was just launched today at http://www.fqxi.org/community/forum.php, so
> please consider copying stuff you post to this list to the Ultimate
> Reality section there.
Thanks for the info.
Best,
Bruno
